题目内容
11.在半径为5cm的⊙O中,圆心O到弦AB的距离为4cm,则弦AB的长为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
分析 利用垂径定理先求出AC=$\frac{1}{2}$AB,再根据勾股定理求AB的长.
解答 解:如图,连接OA;
Rt△OAC中,OA=5cm,OC=4cm;
由勾股定理,得:AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=3cm;
∴AC=$\frac{1}{2}$AB,
∴AB=2AC=6cm;
故选D.
点评 本题考查了勾股定理及垂径定理,垂直于弦的直径平分这条弦,并且平分这条弦所对的两段弧,及勾股定理求解.

练习册系列答案
相关题目
2.当a=-1时,分式$\frac{{{a^2}+a}}{{{a^2}-a}}$( )
| A. | 等于零 | B. | 等于1 | C. | 等于-1 | D. | 没有意义 |
19.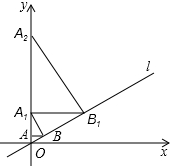 如图,直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点Bn的坐标是( )
如图,直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点Bn的坐标是( )
 如图,直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点Bn的坐标是( )
如图,直线l为正比例函数y=$\frac{\sqrt{3}}{3}$x的图象,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…;按此作法继续下去,则点Bn的坐标是( )| A. | ($\sqrt{3}$×4n,4n) | B. | ($\sqrt{3}$×4n-1,4n-1) | C. | ($\sqrt{3}$×4n-1,4n) | D. | ($\sqrt{3}$×4n,4n-1) |
20. 已知一块蓄电池的电压为定值,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )
已知一块蓄电池的电压为定值,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )
 已知一块蓄电池的电压为定值,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )
已知一块蓄电池的电压为定值,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )| A. | I=$\frac{32}{R}$ | B. | I=-$\frac{32}{R}$ | C. | I=$\frac{4}{R}$ | D. | I=$\frac{8}{R}$ |
1.某品牌手机,去年每台的售价y(元)与月份x之间满足关系y=-50x+2600,去年的月销量p(万元)与月份x之间成一次函数关系,其中第一季度的销量情况如表:
(1)求p关于x的函数关系式;
(2)求去年12月份的销售量与销售价格;
(3)今年1月份比去年12月份该品牌手机的售价下降的百分率为m,销售量下降的百分率为1.5m,今年2月份,经销商对该手机以1月份价格的八折销售,这样2月份的销售量比今年1月份增加了1.5万台,销售额为6400万元,求m的值.
| 月份(x) | 1月 | 2月 | 3月 |
| 销售量(p) | 3.9万台 | 4.0万台 | 4.1万台 |
(2)求去年12月份的销售量与销售价格;
(3)今年1月份比去年12月份该品牌手机的售价下降的百分率为m,销售量下降的百分率为1.5m,今年2月份,经销商对该手机以1月份价格的八折销售,这样2月份的销售量比今年1月份增加了1.5万台,销售额为6400万元,求m的值.
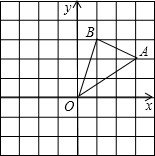 如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A,B的坐标分别是(3,2)、B(1,3).
如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A,B的坐标分别是(3,2)、B(1,3). 如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为50°.
如图,PA、PB分别与⊙O相切于A、B两点,若∠C=65°,则∠P的度数为50°. 如图是边长为2的正方形ABCD,对角线为AC,△ABC以点A为中心,顺时针旋转45°得△AB′C′,则图中阴影部分的面积为4$\sqrt{2}$-4.
如图是边长为2的正方形ABCD,对角线为AC,△ABC以点A为中心,顺时针旋转45°得△AB′C′,则图中阴影部分的面积为4$\sqrt{2}$-4.