题目内容
15.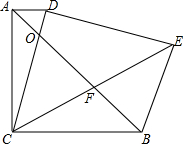 已知如图,△ABC和△DCE都是等腰直角三角形,AC=BC,DC=DE,AD∥BC,CE与AB相交于点F,CD与AB相交于点O,连接BE.探究CF与EF的关系,并证明你的结论.
已知如图,△ABC和△DCE都是等腰直角三角形,AC=BC,DC=DE,AD∥BC,CE与AB相交于点F,CD与AB相交于点O,连接BE.探究CF与EF的关系,并证明你的结论.
分析 连接DF,根据等腰直角三角形的性质证明△AOD∽△COF,根据相似三角形的性质得到$\frac{AO}{CO}$=$\frac{OD}{OF}$,根据相似三角形的判定定理得到△AOC∽△DOF,证明∠CFD=90,根据等腰三角形的性质证明结论.
解答 解:CF=EF,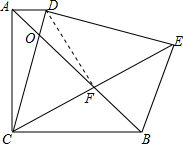
证明:连接DF,
∵AD∥BC,
∴∠DAO=∠ABC=45°,
又∵∠DCF=45°,
∴∠DAO=∠DCF,
又∵∠AOD=∠COB,
∴△AOD∽△COF,
∴$\frac{AO}{CO}$=$\frac{OD}{OF}$,
∴$\frac{AO}{DO}$=$\frac{CO}{FO}$,
又∵∠AOC=∠DOF
∴△AOC∽△DOF,
∴∠CAO=∠CDF=45°,
∴∠CFD=90,
又∵CD=DE,
∴CF=EF.
点评 本题考查的是等腰直角三角形的性质和相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.某市中小学统一组织文艺演出活动,甲、乙两所学校共92人(其中甲校人数多于乙校人数,且甲校人数少于90人)准备统一购买服装参加演出,下面是某服装厂给出的演出服装的价格表:
如果两校分别单独购买服装,一共应付5000元.
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(2)甲、乙两校各有多少学生准备参加演出?
(3)如果甲校有8名同学抽调去参加汉字听写大会而不能参加演出,请为两校设计一种省钱的购买服装方案.
| 购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
| 每套服装的价格 | 60元 | 50元 | 40元 |
(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(2)甲、乙两校各有多少学生准备参加演出?
(3)如果甲校有8名同学抽调去参加汉字听写大会而不能参加演出,请为两校设计一种省钱的购买服装方案.
 如图,在△ABC中,D是BC边上一点,过D点作DE⊥AB于E,DF⊥AC于F,M、N分别是AD,EF的中点.求证:MN⊥EF.
如图,在△ABC中,D是BC边上一点,过D点作DE⊥AB于E,DF⊥AC于F,M、N分别是AD,EF的中点.求证:MN⊥EF.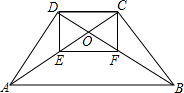 已知如图,等腰梯形ABCD中,AB∥CD,AD=BC,对角线AC与BD交于点O,点E,F分别在OA,OB上,且OC=OE,OD=OF.求证:四边形DEFC是矩形.
已知如图,等腰梯形ABCD中,AB∥CD,AD=BC,对角线AC与BD交于点O,点E,F分别在OA,OB上,且OC=OE,OD=OF.求证:四边形DEFC是矩形.