题目内容
10.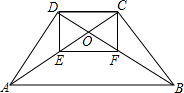 已知如图,等腰梯形ABCD中,AB∥CD,AD=BC,对角线AC与BD交于点O,点E,F分别在OA,OB上,且OC=OE,OD=OF.求证:四边形DEFC是矩形.
已知如图,等腰梯形ABCD中,AB∥CD,AD=BC,对角线AC与BD交于点O,点E,F分别在OA,OB上,且OC=OE,OD=OF.求证:四边形DEFC是矩形.
分析 先证明四边形DEFC是平行四边形,再由等腰梯形的性质得出∠ADC=∠BCD,由SAS证明△ADC≌△BCD,得出对应角相等∠OCD=∠ODC,由等角对等边得出OD=OC,证出CE=DF,即可得出四边形DEFC是矩形.
解答 证明:∵OC=OE,OD=OF,
∴四边形DEFC是平行四边形,
∵四边形ABCD是等腰梯形,
∴∠ADC=∠BCD,
在△ADC和△BCD中,
$\left\{\begin{array}{l}{AD=BC}&{\;}\\{∠ADC=∠BCD}&{\;}\\{CD=DC}&{\;}\end{array}\right.$,
∴△ADC≌△BCD(SAS),
∴∠OCD=∠ODC,
∴OD=OC,
∴OC=OE=OD=OF,
∴CE=DF,
∴四边形DEFC是矩形.
点评 本题考查了等腰梯形的性质、平行四边形的判定、矩形的判定;熟练掌握等腰梯形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
1.给出下列表格:
根据表中信息,y关于x的函数解析式可以是y=3x-2.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -8 | -5 | -2 | 1 | 4 | … |
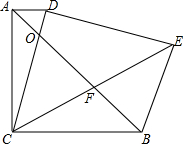 已知如图,△ABC和△DCE都是等腰直角三角形,AC=BC,DC=DE,AD∥BC,CE与AB相交于点F,CD与AB相交于点O,连接BE.探究CF与EF的关系,并证明你的结论.
已知如图,△ABC和△DCE都是等腰直角三角形,AC=BC,DC=DE,AD∥BC,CE与AB相交于点F,CD与AB相交于点O,连接BE.探究CF与EF的关系,并证明你的结论.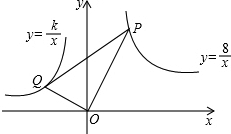 如果y=$\frac{8}{x}$过P点,y=$\frac{k}{x}$过Q点,OP⊥OQ,OP=2OQ,Q(m,1),则S△OPQ=5.
如果y=$\frac{8}{x}$过P点,y=$\frac{k}{x}$过Q点,OP⊥OQ,OP=2OQ,Q(m,1),则S△OPQ=5.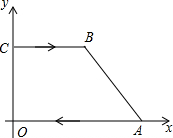 四边形ABCD在坐标系中的坐标为A(8,0),B(6,4),C(0,4),O(0,0),P点在CB上从C点向B点运动,运动速度为每秒2个单位;Q点在AO上从A点向O点运动,运动速度为每秒3个单位,P点和Q点同时运动,其中一点达到终点另一点随即停止运动,设运动时间为t秒
四边形ABCD在坐标系中的坐标为A(8,0),B(6,4),C(0,4),O(0,0),P点在CB上从C点向B点运动,运动速度为每秒2个单位;Q点在AO上从A点向O点运动,运动速度为每秒3个单位,P点和Q点同时运动,其中一点达到终点另一点随即停止运动,设运动时间为t秒