题目内容
16.若|a+2|+|b+c|+|c-4|=0,则abc=32,-a2b2c2=-1024.分析 由非负数的性质可求得a、b、c的值,然后再代入求值即可.
解答 解:∵|a+2|+|b+c|+|c-4|=0,
∴a+2=0,c-4=0,b+c=0.
∴a=-2,c=4,b=-4.
∴abc=-2×(-4)×4=32;-a2b2c2=-(-2)2×(-4)2×42=-1024.
故答案为:32;-1024.
点评 本题主要考查的是非负数的性质、有理数的乘法、乘方、绝对值的性质,求得a、b、c的值是解题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
7.若$\frac{|x|}{x}$=-1,则x是( )
| A. | 正数 | B. | 负数 | C. | 正数或0 | D. | 负数或0 |
4.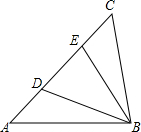 如图,已知△AEB≌△CDB,AE=DC,AB=BC,∠A=50°,∠AEB=70°,则∠CBD=( )
如图,已知△AEB≌△CDB,AE=DC,AB=BC,∠A=50°,∠AEB=70°,则∠CBD=( )
 如图,已知△AEB≌△CDB,AE=DC,AB=BC,∠A=50°,∠AEB=70°,则∠CBD=( )
如图,已知△AEB≌△CDB,AE=DC,AB=BC,∠A=50°,∠AEB=70°,则∠CBD=( )| A. | 50° | B. | 60° | C. | 70° | D. | 无法确定 |
14.点A(-3,y1),B(2,y2)都在直线y=(-a2-1)x+3上,则y1与y2的关系是( )
| A. | y1≤y2 | B. | y1=y2 | C. | y1<y2 | D. | y1>y2 |
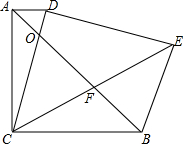 已知如图,△ABC和△DCE都是等腰直角三角形,AC=BC,DC=DE,AD∥BC,CE与AB相交于点F,CD与AB相交于点O,连接BE.探究CF与EF的关系,并证明你的结论.
已知如图,△ABC和△DCE都是等腰直角三角形,AC=BC,DC=DE,AD∥BC,CE与AB相交于点F,CD与AB相交于点O,连接BE.探究CF与EF的关系,并证明你的结论.