题目内容
6．
如图，在△ABC中，D是BC边上一点，过D点作DE⊥AB于E，DF⊥AC于F，M、N分别是AD，EF的中点．求证：MN⊥EF．
分析 根据直角三角形斜边上的中线等于斜边的一半得到ME=MF，根据等腰三角形三线合一证明结论．
解答 证明：
连接ME、MF，
∵DE⊥AB，M是AD的中点，
∴ME=$\frac{1}{2}$AD，
∵DF⊥AC，M是AD的中点，
∴MF=$\frac{1}{2}$AD，
∴ME=MF，又N是EF的中点，
∴MN⊥EF．
点评 本题考查的是直角三角形的性质和等腰三角形的性质，掌握等腰三角形三线合一性质、直角三角形斜边上的中线等于斜边的一半是解题的关键．
练习册系列答案
高中必刷题系列答案
相关题目
7．若$\frac{|x|}{x}$=-1，则x是（ ）
| A． | 正数 | B． | 负数 | C． | 正数或0 | D． | 负数或0 |
14．点A（-3，y1），B（2，y2）都在直线y=（-a2-1）x+3上，则y1与y2的关系是（ ）
| A． | y1≤y2 | B． | y1=y2 | C． | y1＜y2 | D． | y1＞y2 |
1．给出下列表格：
根据表中信息，y关于x的函数解析式可以是y=3x-2．
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -8 | -5 | -2 | 1 | 4 | … |
根据如图所示的程序计算y的值，若输入x的值为$\frac{4}{3}$，则输出y的值时多少？写出你的理由和运算过程．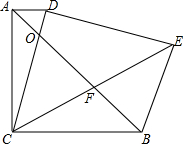
已知如图，△ABC和△DCE都是等腰直角三角形，AC=BC，DC=DE，AD∥BC，CE与AB相交于点F，CD与AB相交于点O，连接BE．探究CF与EF的关系，并证明你的结论．