题目内容
17. 如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AM为∠BAC的平分线,若BC=20cm,则AM的长为$\frac{40}{3}$cm.
如图所示,在Rt△ABC中,∠C=90°,∠BAC=60°,AM为∠BAC的平分线,若BC=20cm,则AM的长为$\frac{40}{3}$cm.
分析 过点M作DM⊥AB于D,根据角平分线上的点到角的两边距离相等可得CM=DM,根据直角三角形两锐角互余求出∠B=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得BM=2DM,然后求出CM,再求出∠CAM=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半可得AM=2CM.
解答  解:如图,过点M作DM⊥AB于D,
解:如图,过点M作DM⊥AB于D,
∵AM为∠BAC的平分线,∠C=90°,
∴CM=DM,
∵∠C=90°,∠BAC=60°,
∴∠B=30°,
∴BM=2DM,
∵BC=20cm,
∴BM+CM=2CM+CM=20,
解得CM=$\frac{20}{3}$cm,
∵∠BAC=60°,AM为∠BAC的平分线,
∴∠CAM=$\frac{1}{2}$∠BAC=30°,
∴AM=2CM=2×$\frac{20}{3}$=$\frac{40}{3}$cm.
故答案为:$\frac{40}{3}$.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,直角三角形30°角所对的直角边等于斜边的一半,熟记两性质并作辅助线构造出含30°角的直角三角形是解题的关键.

练习册系列答案
相关题目

 已知:如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A,B两点,与x轴交于C点,与y轴交于点D,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{2}{5}$.
已知:如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A,B两点,与x轴交于C点,与y轴交于点D,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=$\frac{2}{5}$.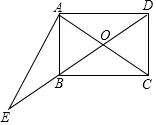 如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则$\frac{AO}{AE}$的值为$\frac{7}{24}$.
如图,在矩形ABCD中,对角线AC,BD交于点O,过点A作EA⊥CA交DB的延长线于点E,若AB=3,BC=4,则$\frac{AO}{AE}$的值为$\frac{7}{24}$.