题目内容
3.已知直线y1=2x和y2=-$\frac{1}{2}$x+3.(1)求这两条直线的交点坐标.
(2)利用图象求当函数y1=-$\frac{1}{2}$x+3的值大于函数y2=2x的值时,x的取值范围.
分析 (1)作出求出方程组的解即可解答;
(2)由(1)中所得交点结合图象即求得.
解答 解:(1)由题意得:$\left\{\begin{array}{l}{y=2x}\\{y=-\frac{1}{2}x+3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{6}{5}}\\{y=\frac{12}{5}}\end{array}\right.$
∴这两条直线的交点坐标为($\frac{6}{5},\frac{12}{5}$).
(2)如图,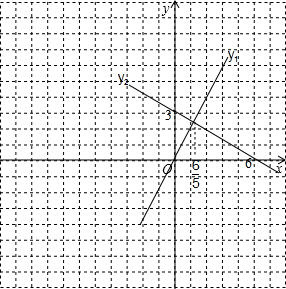
当函数y2=-$\frac{1}{2}$x+3的值大于函数y1=2x的值时,x<$\frac{6}{5}$.
点评 本题考查两直线的相交问题,解决本题的关键是(1)令两直线相等,即可求得两直线的交点坐标.(2)从(1)中得到的交点结合图象即求得.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.已知实数a、b、c满足a+b+c=0,a>b>c,若直线y1=ax+b+c经过抛物线y2=ax2+bx+c的顶点,则下列结论错误的是( )
| A. | 直线y1经过一、三、四象限 | |
| B. | 抛物线y2必经过点(1,0) | |
| C. | 当x>1或x<0时,y2>y1 | |
| D. | 当x>-1时,y1、y2均随x的增大而增大 |
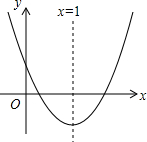 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与y轴的正半轴相交,顶点在第四象限,下列结论:①am2+bm=a(2-m)2+b(2-m);②a+b<0;③$\frac{c}{a}$<1,其中正确的结论个数为( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与y轴的正半轴相交,顶点在第四象限,下列结论:①am2+bm=a(2-m)2+b(2-m);②a+b<0;③$\frac{c}{a}$<1,其中正确的结论个数为( )
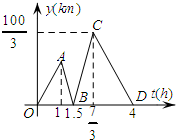 甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为($\frac{7}{3},\frac{100}{3}$),请解决以下问题:
甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为($\frac{7}{3},\frac{100}{3}$),请解决以下问题: