题目内容
16.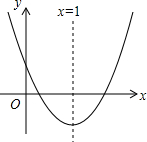 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与y轴的正半轴相交,顶点在第四象限,下列结论:①am2+bm=a(2-m)2+b(2-m);②a+b<0;③$\frac{c}{a}$<1,其中正确的结论个数为( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,与y轴的正半轴相交,顶点在第四象限,下列结论:①am2+bm=a(2-m)2+b(2-m);②a+b<0;③$\frac{c}{a}$<1,其中正确的结论个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据二次函数对称轴判断出m与2-m关于对称轴对称,从而确定出①正确;根据二次函数图象开口向上判断出a>0,再根据二次函数的对称轴得到a、b的关系,然后整理即可得到a+b<0,判断出②正确;令x=1得到a、b、c的不等式,然后消掉b整理即可判断出③正确.
解答 解:∵抛物线对称轴为直线x=1,m与2-m关于直线x=1对称,
∴am2+bm=a(2-m)2+b(2-m),故①正确;
∵抛物线开口向上,
∴a>0,
∵对称轴为直线x=1,
∴-$\frac{b}{2a}$=1,
∴b=-2a,
∴a+b=a-2a=-a<0,故②正确;
∵对称轴为直线x=1,顶点在第四象限,
∴x=1时,a+b+c<0,
∴a-2a+c<0,
∴c<a,
∴$\frac{c}{a}$<1,故③正确,
综上所述,结论正确的有3个.
故选D.
点评 本题考查了二次函数的性质,主要利用了二次函数的对称性,对称轴的表示,此类题目,利用自变量的特殊值求解是常用的方法之一.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
7.某玩具店试销售一种进价为20元的新型玩具,根据物价部门规定:该玩具售价不得超过90元.在连续七天的试销售过程中,玩具店就销售量y(个)与售价x(元)之间的变化关系做了如表记录.
(1)运用所学过的函数知识,试判断y与x之间的函数关系,并求y与x的函数关系式;
(2)该玩具店若想每天获得2400元的利润,应将售价定为多少元?
(3)这种新型玩具的售价定为多少元时,玩具店每天能够获得的利润w(元)最大?此时的最大利润为多少元?
| 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 | |
| 售价x | 30 | 30 | 35 | 40 | 40 | 40 | 45 |
| 销售量y | 100 | 100 | 95 | 90 | 90 | 90 | 85 |
(2)该玩具店若想每天获得2400元的利润,应将售价定为多少元?
(3)这种新型玩具的售价定为多少元时,玩具店每天能够获得的利润w(元)最大?此时的最大利润为多少元?
11.下列各数中,最小的数是( )
| A. | -3 | B. | 1 | C. | 0 | D. | 2 |
 如图,△ABC在方格中位置如图所示,A(1,4),B(-2,2).
如图,△ABC在方格中位置如图所示,A(1,4),B(-2,2).