题目内容
13.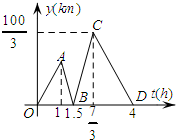 甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为($\frac{7}{3},\frac{100}{3}$),请解决以下问题:
甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为($\frac{7}{3},\frac{100}{3}$),请解决以下问题:(1)甲比乙晚出发1h;
(2)分别求出甲、乙二人的速度;
(3)丙骑摩托车与乙同时出发,从N地沿同一条公路匀速前往M地,若丙经过$\frac{4}{3}$h与乙相遇.
①设丙与M地的距离为S(km),行驶的时间为t(h),求S与t之间的函数关系式(不用写自变量的取值范围)
②丙与乙相遇后再用多少时间与甲相遇.
分析 (1)根据图象即可直接作出判断;
(2)根据OA段和AB段时间的关系可求得甲、乙速度之间的关系,然后根据BC段,两人所走的路程的差是$\frac{100}{3}$km,所用的时间已知,即可列方程求解;
(3)①利用待定系数法即可求得函数的解析式;
②利用甲和丙的路程与时间之间的关系式组成方程组,求得甲、丙相遇的时间,则相遇的时间即可求得.
解答 解:(1)1 h;
(2)由图1可知甲、乙在乙出发1.5小时后相遇,
因为甲比乙晚出发1小时,
所以甲仅用0.5小时走了乙用1.5小时所用的路程,
所以甲的速度是乙的速度的3倍.
设乙的速度为xkm/h,
则甲的速度为3xkm/h,由图1得:(3x-x)•($\frac{7}{3}$-1.5)=$\frac{100}{3}$;
解得:x=20,
所以乙的速度为20km/h,甲的速度为60 km/h,
(3)①设s=kt+b.当$t=\frac{4}{3}$时,$S=\frac{4}{3}×20=\frac{80}{3}$;
当t=0时,S=20×4=80;代入得k=-40,b=80
故丙距M地的路程S与时间t的函数关系式为S=-40t+80.
②由甲的速度为60 km/h且比乙晚出发一小时易得S甲=60t-60,与S丙=-40t+80,
联立$\left\{\begin{array}{l}S=60t-60\\ S=-40t+80\end{array}\right.$,
解得t=$\frac{7}{5}$,即在丙出发$\frac{7}{5}$小时后,甲、丙相遇.
∵$\frac{7}{5}-\frac{4}{3}=\frac{1}{15}$,
∴丙与乙相遇后再用$\frac{1}{15}h$与甲相遇.
点评 本题考查了函数的图象以及待定系数法求一次函数的解析式,求得三个人对应的路程与时间之间的函数关系式是关键.

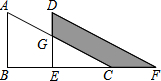 如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$.
如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$. 如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与正比例函数y=-2x的图象相交于点A,且与x轴交于点B,求这个一次函数的解析式.
如图,在平面直角坐标系内,一次函数y=kx+b(k≠0)的图象与正比例函数y=-2x的图象相交于点A,且与x轴交于点B,求这个一次函数的解析式.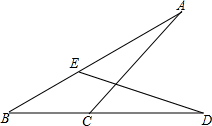 如图,已知AC=DE,AB=BD,求证:BC=BE.
如图,已知AC=DE,AB=BD,求证:BC=BE. 如图,直线y=2x-4分别交坐标轴于A、B两点,交双曲线y=$\frac{k}{x}$(x>0)于C点,且sin∠COB=$\frac{\sqrt{2}}{2}$.
如图,直线y=2x-4分别交坐标轴于A、B两点,交双曲线y=$\frac{k}{x}$(x>0)于C点,且sin∠COB=$\frac{\sqrt{2}}{2}$.