题目内容
5.某商店购进某种商品的价格是2.5元/件,在一段时间里,单价是13.5元,销售量是500件,而单价每降低1元就可多售出200件,当销售价为x元/件时,获利润w元,则w与x的函数关系为( )| A. | w=-200x2+3700x-80000 | B. | w=-200x2+3200x | ||
| C. | w=-200x2-800 | D. | 以上答案都不对 |
分析 当销售价为x元/件时,每件利润为(x-2.5)元,销售量为[500+200×(13.5-x)],根据利润=每件利润×销售量列出函数关系式即可.
解答 解:由题意得w=(x-2.5)×[500+200×(13.5-x)],
整理得:w=-200x2+3700x-8000.
故选D.
点评 本题考查了根据实际问题列二次函数关系式,用含x的代数式分别表示出每件利润及销售量是解题的关键.

练习册系列答案
相关题目
17. 如图所示,作出正五边形的所有对角线,得到一个五角星,那么,在五角星含有的多边形中( )
如图所示,作出正五边形的所有对角线,得到一个五角星,那么,在五角星含有的多边形中( )
 如图所示,作出正五边形的所有对角线,得到一个五角星,那么,在五角星含有的多边形中( )
如图所示,作出正五边形的所有对角线,得到一个五角星,那么,在五角星含有的多边形中( )| A. | 只有三角形 | |
| B. | 只有三角形和四边形 | |
| C. | 只有三角形,四边形和五边形 | |
| D. | 只有三角形,四边形,五边形和六边形 |
14.在Rt△ABC中,∠C=90°,若tan$\frac{B}{2}$=$\frac{\sqrt{3}}{3}$,则sinB的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
 如图,在?ABCD中,A(1,0),B(0,-2),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,D在y轴上,若?ABCD的面积为6,求k的值.
如图,在?ABCD中,A(1,0),B(0,-2),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,D在y轴上,若?ABCD的面积为6,求k的值.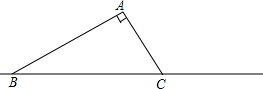 已知,如图,在△ABC中,AC=3厘米,BC=6厘米,∠C=60°,求:
已知,如图,在△ABC中,AC=3厘米,BC=6厘米,∠C=60°,求: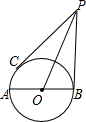 如图,已知点C在以AB为直径的⊙O上,过点B、C作⊙O的切线,且交于点P,联结AC,若OP=$\frac{9}{2}$AC.求$\frac{PB}{AC}$的值.
如图,已知点C在以AB为直径的⊙O上,过点B、C作⊙O的切线,且交于点P,联结AC,若OP=$\frac{9}{2}$AC.求$\frac{PB}{AC}$的值.