题目内容
13.用分式填空:①某食堂有煤m吨,原计划每天烧煤a吨,现每天节约用煤b(b<a)吨,则这批煤可比原计划多烧($\frac{m}{a-b}$-$\frac{m}{a}$)天.
②小明参加打靶比赛,有a次打了m环,b次打了n环,则此次打靶的平均成绩是$\frac{am+bn}{a+b}$环.
③有一大捆粗细均匀的电线,现要确定其长度,于是从中抽出1米长的电线,称出它的质量为a,而其余电线的总质量为b,则这捆电线的总长度为$\frac{a+b}{a}$米.
分析 ①先分别表示出原计划烧的天数和实际烧的天数,然后求它们的差即可;
②用两次的总环数除以总打靶次数即可得到此次打靶的平均成绩;
③用质量(a+b)除以a后再乘以1米可得到这捆电线的总长度.
解答 解:①这批煤可比原计划多烧的天数为($\frac{m}{a-b}$-$\frac{m}{a}$)天;
②此次打靶的平均成绩=$\frac{am+bn}{a+b}$(环);
③这捆电线的总长度为$\frac{a+b}{a}$(米).
故答案为($\frac{m}{a-b}$-$\frac{m}{a}$);=$\frac{am+bn}{a+b}$环;$\frac{a+b}{a}$.
点评 本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
5.某商店购进某种商品的价格是2.5元/件,在一段时间里,单价是13.5元,销售量是500件,而单价每降低1元就可多售出200件,当销售价为x元/件时,获利润w元,则w与x的函数关系为( )
| A. | w=-200x2+3700x-80000 | B. | w=-200x2+3200x | ||
| C. | w=-200x2-800 | D. | 以上答案都不对 |
3.一次函数y=2x-1的图象可以由一次函数y=2x+3的图象( )
| A. | 向右平移4个单位长度得到 | B. | 向左平移2个单位长度得到 | ||
| C. | 向上平移2个单位长度得到 | D. | 向下平移4个单位长度得到 |
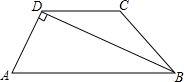 如图,等腰梯形ABCD,AB∥DC,AB=2,∠ADB=90°.
如图,等腰梯形ABCD,AB∥DC,AB=2,∠ADB=90°.