题目内容
15. 如图,在?ABCD中,A(1,0),B(0,-2),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,D在y轴上,若?ABCD的面积为6,求k的值.
如图,在?ABCD中,A(1,0),B(0,-2),反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,D在y轴上,若?ABCD的面积为6,求k的值.
分析 根据A(1,0),B(0,-2),得到OA=1,O2,根据?ABCD的面积为6,求出BD=6,得到D(0,4),根据平行四边形的性质得到CD=AB,CD∥AB,推出△CDE≌△ABO,根据全等三角形的性质得到CE=AO=1,DE=BO=2,求出C(-1,2),即可得到结论.
解答  解:∵A(1,0),B(0,-2),
解:∵A(1,0),B(0,-2),
∴OA=1,O2,
∵?ABCD的面积为6,
∴S△ABD=$\frac{1}{2}$?ABCD的面积=3,
∴BD=6,
∴OD=4,
∴D(0,4),
∵四边形ABCD是平行四边形,
∴CD=AB,CD∥AB,
∴∠CDE=∠ABO,
过C作CE⊥BD于E,
在△CDE与△ABO中,$\left\{\begin{array}{l}{∠CDE=∠ABO}\\{∠DEC=∠AOB=90°}\\{CD=AB}\end{array}\right.$,
∴△CDE≌△ABO,
∴CE=AO=1,DE=BO=2,
∴OE=2,
∴C(-1,2),
∵反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,
∴k=-2.
点评 本题考查了平行四边形的性质,全等三角形的判定和性质,反比例函数图象上点的坐标特征,熟练掌握平行四边形的性质是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
5.某商店购进某种商品的价格是2.5元/件,在一段时间里,单价是13.5元,销售量是500件,而单价每降低1元就可多售出200件,当销售价为x元/件时,获利润w元,则w与x的函数关系为( )
| A. | w=-200x2+3700x-80000 | B. | w=-200x2+3200x | ||
| C. | w=-200x2-800 | D. | 以上答案都不对 |
 在△ABC中点D是BC上一点,∠BAC=90°,∠C=30°,作AC的中垂线DE交BC于D点,连接AD,求证:△ABD是等边三角形.
在△ABC中点D是BC上一点,∠BAC=90°,∠C=30°,作AC的中垂线DE交BC于D点,连接AD,求证:△ABD是等边三角形. 如图,正方形网络中小方格的边长为1,A、B、C都是格点.
如图,正方形网络中小方格的边长为1,A、B、C都是格点.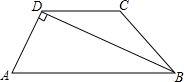 如图,等腰梯形ABCD,AB∥DC,AB=2,∠ADB=90°.
如图,等腰梯形ABCD,AB∥DC,AB=2,∠ADB=90°.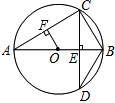 如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F,
如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F,