题目内容

1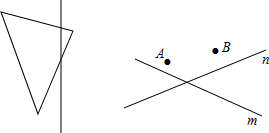．（1）以直线为对称轴，画出下列图形的另一部分使它们成为轴对称图形．
（2）如图，求作点P，使点P同时满足：①PA=PB；②到直线m，n的距离相等．（尺规作图，保留作图痕迹）

分析 （1）分别作出A、B、C关于直线MN的对称点即可．
（2）作线段AB的垂直平分线，直线m、n组成的角的平分线，两线的交点就是所求的点．

解答 解：（1）如图1中，作点A关于直线MN的对称点E，点B关于直线MN的对称点F，点C关于直线NM的对称点G，
连接EF、FG．EG，△EFG就是所求作的三角形．


（2）如图2中，图中点P和点P′就是满足条件的点．

点评 本题考查轴对称-作图变换、线段垂直平分线的性质，角平分线的性质等知识，解题的关键是熟练掌握这些基本作图，属于中考常考题型．

练习册系列答案
相关题目
17．如图是四届世界数学家大会的会标，其中是轴对称图形的是（　　）
A．B．C．D．
18．方程组$\left\{\begin{array}{l}{3x+5y=2}\\{2x+4y=6}\end{array}\right.$的解适合x+y=a，则a的值等于（　　）
A．-2B．3C．4D．-4
9．规定x=x0时，代数式$\frac{x^2}{{1+{x^2}}}$的值记为f（x0）．例如：x=-1时，$f（-1）=\frac{{{{（-1）}^2}}}{{1+{{（-1）}^2}}}=\frac{1}{2}$，则$f（1）+f（2）+f（3）+…+f（168）+f（\frac{1}{2}）+f（\frac{1}{3}）+f（\frac{1}{4}）+…+f（\frac{1}{168}）$的值等于167$\frac{1}{2}$．
16．已知$a=\frac{\sqrt{3}-1}{2}$，则$\frac{2{a}^{3}+6{a}^{2}+a}{2{a}^{2}-1}$=（　　）
A．-$\sqrt{3}$B．$\sqrt{3}$C．$-\sqrt{3}+2$D．$\sqrt{3}$+2
6．星期日上午小明骑车去姥姥家吃午饭．已知从小明家去姥姥家的路是上坡路，吃过午饭后，下午按原路返回，设小明从家出发后所用的时间为x（小时），骑车所走的路程为y（千米），则y与x的函数图象大致是（　　）
A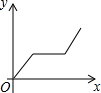．B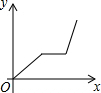．C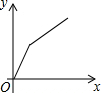．D．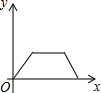
13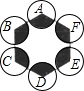．如图，正六边形的边长为10，分别以正六边形的顶点A、B、C、D、E、F为圆心，画6个全等的圆．若圆的半径为x，且0＜x≤5，阴影部分的面积为y，能反映y与x之间函数关系的大致图形是（　　）
A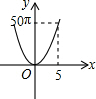．B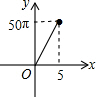．C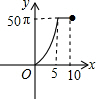．D．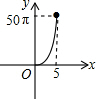
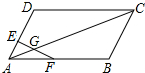10．某次器乐比赛设置了6个获奖名额，共有ll名选手参加，他们的比赛得分均不相同．若 知道了某位选手的得分，要判断他能否获奖，只需知道这ll名选手成绩的统计量中的（　　）
A．众数B．中位数C．平均数D．方差
11．如图，点E为?ABCD的AD边上一点，且AE：ED=1：3，点F为AB的中点，EF交AC于点G，则AG：GC等于1：5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网