题目内容
15．
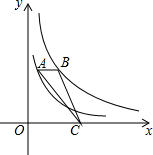如图，点A在双曲线y=$\frac{2}{x}$上，点B在双AB曲线y=$\frac{5}{x}$上．点C是x轴上一动点．若AB∥x轴．则△ABC的面积为1.5．
分析 作AE⊥x轴于E，BF⊥x轴于F，延长BA交y轴于点D，如图，根据反比例函数比例系数k的几何意义得S矩形AEOD=2，S矩形BFOD=5，于是得到S矩形AEFB=3，然后根据矩形的性质和三角形面积公式易得S△ABC=S△FAB=1.5．
解答 解：作AE⊥x轴于E，BF⊥x轴于F，延长BA交y轴于点D，如图，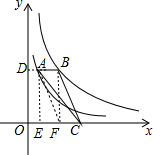
∵AB∥x轴，
∴S矩形AEOD=2，S矩形BFOD=5，
∴S矩形AEFB=5-2=3，
∴S△FAB=1.5，
∴S△ABC=S△FAB=1.5．
故答案为1.5．
点评 本题考查了反比例函数比例系数k的几何意义：在反比例函数y=$\frac{k}{x}$图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．在反比例函数的图象上任意一点象坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|，且保持不变．解决本题的关键是把求△ABC的面积转化为求△FAB的面积．
练习册系列答案
相关题目
10．有一箱子装有3张分别标示4，5，6的号码牌，已知小明以每次取一张且取后不放回的方式，先后取出2张牌，组成一个二位数，则组成的二位数是6的倍数的概率是（ ）
| A． | $\frac{7}{12}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
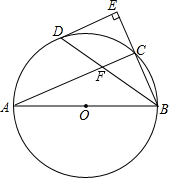如图，已知AB为⊙O的直径，C为⊙O上异于A、B的一个动点，作∠ABC的平分线交⊙O于点D，过点D作⊙O的切线与BC的延长线交于点E，连接BD交AC于点F，小明经操作发现如下2个结论：①∠E为直角；②FA=FB，请你分别判断这两个结论是否成立？若成立，请给予证明；若不成立，请补充条件，使之成立．
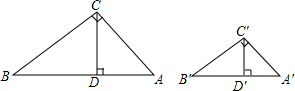如图，在Rt△ABC和Rt△A′B′C′中，∠ACB=∠A′B′C′中，∠ACB=∠A′C′B′=90°，CD，C′D′分别是两个三角形斜边上的高，且CD：C′D′=AC：A′C′．证明：△ABC∽△A′B′C′．
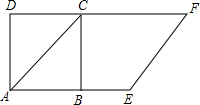如图，以正方形ABCD的对角线AC为一边，延长AB到E，使AE=AC，以AE为一边作菱形AEFC，若菱形的面积为9$\sqrt{2}$cm2，则正方形ABCD的面积为9．
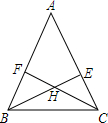已知：如图，BE和CF是△ABC的高线，BE=CF，H是CF、BE的交点．求证：HB=HC．
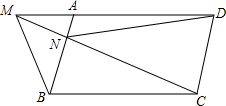已知M是?ABCD的DA边的延长线上任一点，连结MC交AB于N，求证：S△MNB=S△AND．