题目内容
10.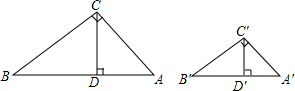 如图,在Rt△ABC和Rt△A′B′C′中,∠ACB=∠A′B′C′中,∠ACB=∠A′C′B′=90°,CD,C′D′分别是两个三角形斜边上的高,且CD:C′D′=AC:A′C′.证明:△ABC∽△A′B′C′.
如图,在Rt△ABC和Rt△A′B′C′中,∠ACB=∠A′B′C′中,∠ACB=∠A′C′B′=90°,CD,C′D′分别是两个三角形斜边上的高,且CD:C′D′=AC:A′C′.证明:△ABC∽△A′B′C′.思路探究:
(1)要证明△ABC∽△A′B′C′,需要证明∠A=∠A′.
(2)要证明(1)中的条件,需证明△ADC∽△A′D′C′.
证明:
分析 (1)利用“两角法”来证明△ABC∽△A′B′C′;
(2)利用相似三角形△ADC∽△A′D′C′的对应角相等证明(1)中的条件.
解答 证明:∵CD、C′D′分别是两个三角形斜边上的高,
∴∠ADC=∠A′D′C′=90°,
∵CD:C′D′=AC:A′C′,
∴△ADC∽△A′D′C′,
∴∠A=∠A′,
∵∠C=∠C′=90°,
∴△ABC∽△A′B′C′.
故答案是:∠A=∠A′;△ADC∽△A′D′C′.
点评 本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.

练习册系列答案
相关题目
 在边长为1的小正方形网格中,△AOB的顶点均在格点上,
在边长为1的小正方形网格中,△AOB的顶点均在格点上,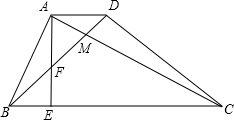 如图:四边形ABCD中,AB=AD,对角线AC,BD相交于点M,且AC⊥AB,BD⊥CD,过点A作AE⊥BC,垂足为E,交BD于点F.
如图:四边形ABCD中,AB=AD,对角线AC,BD相交于点M,且AC⊥AB,BD⊥CD,过点A作AE⊥BC,垂足为E,交BD于点F.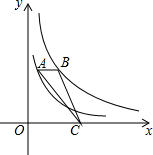 如图,点A在双曲线y=$\frac{2}{x}$上,点B在双AB曲线y=$\frac{5}{x}$上.点C是x轴上一动点.若AB∥x轴.则△ABC的面积为1.5.
如图,点A在双曲线y=$\frac{2}{x}$上,点B在双AB曲线y=$\frac{5}{x}$上.点C是x轴上一动点.若AB∥x轴.则△ABC的面积为1.5.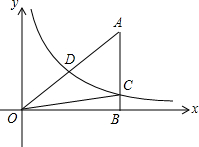 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象交Rt△OAB的斜边OA于点D,交直角边AB于点C,点B在x轴上,若△OAC的面积为5,OA:OD=2:1,则k的值为8.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象交Rt△OAB的斜边OA于点D,交直角边AB于点C,点B在x轴上,若△OAC的面积为5,OA:OD=2:1,则k的值为8.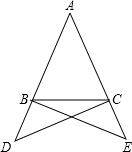 如图,在△ABC中,AB=AC,点D、E分别在AB、AC的延长线上,且∠BCD=$\frac{1}{3}$∠ACB,∠CBE=$\frac{1}{3}$∠ABC.求证:BE=CD.
如图,在△ABC中,AB=AC,点D、E分别在AB、AC的延长线上,且∠BCD=$\frac{1}{3}$∠ACB,∠CBE=$\frac{1}{3}$∠ABC.求证:BE=CD.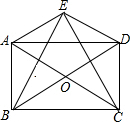 如图,点E为?ABCD外一点,AE⊥EC,BE⊥ED,对角线AC、BD相交于点O.
如图,点E为?ABCD外一点,AE⊥EC,BE⊥ED,对角线AC、BD相交于点O.