题目内容
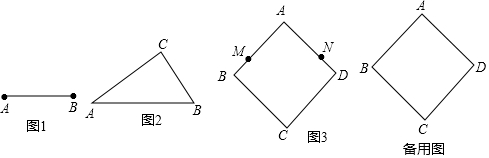
20.将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和不可能是( )| A. | 900° | B. | 360° | C. | 540° | D. | 720° |
分析 根据题意列出可能情况,再分别根据多边形的内角和定理进行解答即可.
解答 解:①将矩形沿对角线剪开,得到两个三角形,两个多边形的内角和为:180°+180°=360°;
②将矩形从一顶点剪向对边,得到一个三角形和一个四边形,两个多边形的内角和为:180°+360°=540°;
③将矩形沿一组对边剪开,得到两个四边形,两个多边形的内角和为:360°+360°=720°,
④将矩形沿一组邻边剪开,得到一个三角形和一个五边形,其内角和为:180°+540°=720°;
故这两个多边形的内角和不可能是900°.
故选:A.
点评 本题考查了多边形的内角与外角,能够得出一个矩形截一刀后得到的图形有三种情形,是解决本题的关键.

练习册系列答案
相关题目
8.下列语句中,是真命题的是( )
| A. | 若ab>0,则a>0,b>0 | B. | 若ab=0,则a=0或b=0 | ||
| C. | 内错角相等 | D. | 相等的角是对顶角 |
12.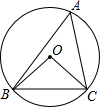 如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )
如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )
 如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )
如图,点O是△ABC内部一点,⊙O经过△ABC的顶点A、B、C,若∠BCO=45°,则∠BAC的大小为( )| A. | 22.5° | B. | 35° | C. | 45° | D. | 67.5° |
10.如图1,菱形纸片ABCD的边长为2,∠ABC=60°,将菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上一点P(如图2),则六边形AEFCHG面积的最大值是( )
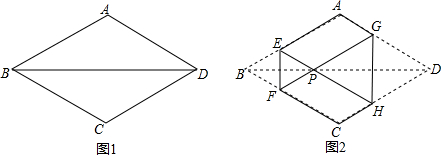

| A. | $\frac{3\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | 2-$\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
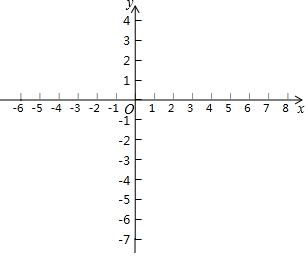 已知:直线y=-$\frac{1}{2}$x+2与x轴交于点A,直线y=3x-1与x轴交于点B,与y轴交于点C,两直线交于点D
已知:直线y=-$\frac{1}{2}$x+2与x轴交于点A,直线y=3x-1与x轴交于点B,与y轴交于点C,两直线交于点D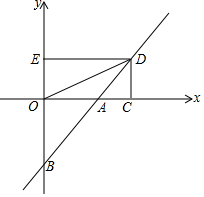 如图,直线y=x+b(b≠0)交坐标轴于A、B两点,点D(2,n)在直线AB上,过D作两坐标的垂线DC、DE,垂足分别为C,E,连接OD.若四边形OCDE的面积为2,
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,点D(2,n)在直线AB上,过D作两坐标的垂线DC、DE,垂足分别为C,E,连接OD.若四边形OCDE的面积为2,