题目内容
15.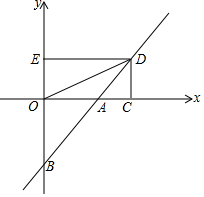 如图,直线y=x+b(b≠0)交坐标轴于A、B两点,点D(2,n)在直线AB上,过D作两坐标的垂线DC、DE,垂足分别为C,E,连接OD.若四边形OCDE的面积为2,
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,点D(2,n)在直线AB上,过D作两坐标的垂线DC、DE,垂足分别为C,E,连接OD.若四边形OCDE的面积为2,(1)求点D的坐标和直线AB的解析式;
(2)点M是直线OD上的一点(不与点O、D重合)且点M的横坐标为m(m>0),求△OCM的面积S与m之间的关系式.
分析 (1)根据已知条件得到四边形OCDE是矩形,根据矩形的面积得到D(2,1),把D(2,1)代入y=x+b得1=2+b,即可得到结论;
(2)根据D(2,1),求得直线OD的解析式为y=$\frac{1}{2}$x,得到M(m,$\frac{1}{2}$m),根据三角形的面积公式即可得到结论.
解答 解:(1)∵DE⊥y轴,CD⊥x轴,
∵∠EOC=90°,
∴四边形OCDE是矩形,
∵D(2,n),四边形OCDE的面积为2,
∴2n=2,
∴n=1,
∴D(2,1),
把D(2,1)代入y=x+b得1=2+b,
∴b=-1,
∴直线AB的解析式为:y=x-1;
(2)∵D(2,1),
∴直线OD的解析式为y=$\frac{1}{2}$x,
∵点M是直线OD上的一点(不与点O、D重合)且点M的横坐标为m,
∴M(m,$\frac{1}{2}$m),
∴S=$\frac{1}{2}$×2×$\frac{1}{2}$m=$\frac{1}{2}$m,(0<m≤2).
点评 本题考查了待定系数法求一次函数解析式,矩形的性质,三角形面积的计算,正确的理解题意是解题的关键.

练习册系列答案
相关题目
3.若分式$\frac{{{x^2}-1}}{{{x^2}-2x-3}}$的值为0,则x的值为( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 0 |
10.下列说法正确的有( )
①$\sqrt{31}$-2的值在3和4之间;
②当a=1时,关于x的一元二次方程x2+2x-a=0有两个相等的实数根;
③命题“对顶角相等”的逆命题是真命题;
④十边形的内角和为1440°;
⑤等边三角形既是轴对称图形又是中心对称图形.
①$\sqrt{31}$-2的值在3和4之间;
②当a=1时,关于x的一元二次方程x2+2x-a=0有两个相等的实数根;
③命题“对顶角相等”的逆命题是真命题;
④十边形的内角和为1440°;
⑤等边三角形既是轴对称图形又是中心对称图形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.将一矩形纸片沿一条直线剪成两个多边形,那么这两个多边形的内角和不可能是( )
| A. | 900° | B. | 360° | C. | 540° | D. | 720° |
 如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )
如图是由4个大小相同的正方体组合而成的几何体,其俯视图是( )






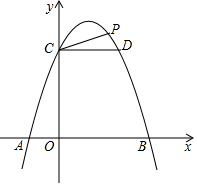 二次函数y=-x2+2x+3的图象与x轴交于A,B两点(点A在B的左侧),与y轴交于点C,过点C作y轴的垂线交抛物线于另一点D.
二次函数y=-x2+2x+3的图象与x轴交于A,B两点(点A在B的左侧),与y轴交于点C,过点C作y轴的垂线交抛物线于另一点D.