题目内容
12．
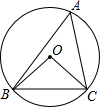如图，点O是△ABC内部一点，⊙O经过△ABC的顶点A、B、C，若∠BCO=45°，则∠BAC的大小为（ ）| A． | 22.5° | B． | 35° | C． | 45° | D． | 67.5° |
分析 判断出△OBC是等腰三角形，根据∠BCO=45°判断出∠OBC的度数，然后求出∠O的度数，再根据圆周角定理求出∠BAC的度数．
解答 解：∵OC=OB，∠BCO=45°，
∴∠OBC=45°，
∴∠BOC=180°-45°-45°=90°，
∴∠BAC=90°×$\frac{1}{2}$=45°，
故选C．
点评 本题考查了圆周角定理，要知道，同弧所对的圆周角等于它所对圆心角的一半．
练习册系列答案
小学教材完全解读系列答案
相关题目
2．
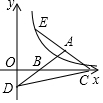如图，等腰三角形ABC的底边BC在x轴正半轴上，点A在第一象限，延长AB交y轴负半轴于点D，延长CA到点E，使AE=AC，双曲线y=$\frac{k}{x}$（x＞0）的图象过点E．若△BCD的面积为2$\sqrt{2}$，则k的值为（ ）
如图，等腰三角形ABC的底边BC在x轴正半轴上，点A在第一象限，延长AB交y轴负半轴于点D，延长CA到点E，使AE=AC，双曲线y=$\frac{k}{x}$（x＞0）的图象过点E．若△BCD的面积为2$\sqrt{2}$，则k的值为（ ）| A． | 4$\sqrt{2}$ | B． | 4 | C． | 2$\sqrt{2}$ | D． | 2 |
3．若分式$\frac{{{x^2}-1}}{{{x^2}-2x-3}}$的值为0，则x的值为（ ）
| A． | -1 | B． | 1 | C． | ±1 | D． | 0 |
20．将一矩形纸片沿一条直线剪成两个多边形，那么这两个多边形的内角和不可能是（ ）
| A． | 900° | B． | 360° | C． | 540° | D． | 720° |
17．
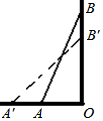如图，梯子AB靠在墙上，梯子底端A到墙根O的距离为2m，梯子的顶端B到地面的距离为7m，现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于3m，同时梯子的顶端B下降至B′，那么BB′（ ）
如图，梯子AB靠在墙上，梯子底端A到墙根O的距离为2m，梯子的顶端B到地面的距离为7m，现将梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于3m，同时梯子的顶端B下降至B′，那么BB′（ ）| A． | 小于1 m | B． | 大于1 m | C． | 等于1 m | D． | 小于或等于1 m |
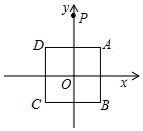如图，在平面直角坐标系中，正方形ABCD的顶点A（1，1），B（1，-1），C（-1，-1），D（-1，1），y轴上有一点P（0，2），作点P关于点A的对称点P1，作点P1关于点B的对称点P2，作点P2关于点C的对称点P3，作点P3关于点D的对称点P4，作点P4关于点A的对称点P5，作点P5关于点B的对称点P6，…，按此规律操作下去，则点P2017的坐标为（ ）