题目内容
20. 实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{a^2}$=b.
实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{a^2}$=b.
分析 根据数轴得出a<0<b,即可知a-b<0,根据绝对值的性质和二次根式的性质即可化简原式.
解答 解:由数轴可知a<0<b,
∴a-b<0,
则原式=-(a-b)-(-a)=-a+b+a=b,
故答案为:b.
点评 本题主要考查实数和数轴、二次根式的性质和绝对值的性质,熟练掌握二次根式的性质:$\sqrt{{a}^{2}}$=|a|是解题的关键.

练习册系列答案
相关题目
10.有x支球队参加篮球比赛,共比赛了21场,每两队之间都比赛一场,则下列方程中符合题意的是( )
| A. | x(x-1)=21 | B. | x(x+1)=21 | C. | x(x-1)=42 | D. | x(x+1)=42 |
11.已知直线y-kx+k=0与直线ky+x-2k=0的交点在y轴上,则k的值为( )
| A. | -2 | B. | 2 | C. | -1 | D. | 1 |
9.在下列调查中,适宜采用普查的是( )
| A. | 对我省七年级学生视力情况的调查 | |
| B. | 对一批LED节能灯使用寿命的调查 | |
| C. | 对量子通信卫星上零部件质量的调查 | |
| D. | 对“最强大脑”节目收视率的调查 |
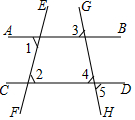 如图,已知∠1=∠2,试说明∠3=∠5.请你把说理过程补充完整.
如图,已知∠1=∠2,试说明∠3=∠5.请你把说理过程补充完整.