题目内容
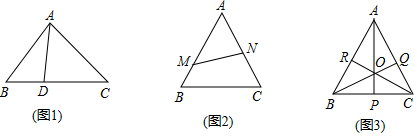
5.自学:如图1,△ABC中,D是BC边上一点,则△ABD与△ADC有一个相同的高,它们的面积之比等于相应的底之比,记为$\frac{{S}_{△ABD}}{{S}_{△ADC}}$=$\frac{BD}{DC}$.(△ABD,△ADC的面积分别用记号S△ABD,S△ADC表示)
心得:如图1,若BD=$\frac{1}{2}$DC,则S△ABD:S△ADC=1:2
成长:如图2,△ABC中,M,N分别是AB,AC边上一点,且有AM:MB=2:1,AN:NC=1:1,则△AMN与△ABC的面积比为1:3.
巅峰:如图3,△ABC中,P,Q,R分别是BC,CA,AB边上的点,且AP,BQ,CR相交于点O,现已知△BPO,△PCO,△COQ,△AOR的面积依次为40,30,35,84,求△ABC的面积.
分析 心得:根据两个三角形有一个相同的高,它们的面积之比等于相应的底之比进行计算即可;
成长:连接BN,根据题意求出S△ANB=S△CNB=$\frac{1}{2}$S△ABC,SAMN=$\frac{2}{3}$S△ANB,计算即可;
巅峰:设△BRO和△AOQ的面积分别为x、y,根据题意列出二元一次方程组,解方程组即可.
解答 解:心得:∵BD=$\frac{1}{2}$DC,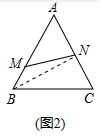
∴$\frac{BD}{DC}$=$\frac{1}{2}$,
∴S△ABD:S△ADC=1:2,
故答案为:1:2;
成长:如图②.连接BN,
∵AN:NC=1:1,
∴S△ANB=S△CNB=$\frac{1}{2}$S△ABC,
∵AM:MB=2:1,
∴SAMN=$\frac{2}{3}$S△ANB,
∴△AMN与△ABC的面积比为1:3,
故答案为:1:3;
巅峰:设△BRO和△AOQ的面积分别为x、y,
∵△BPO,△PCO的面积分别为40,30,
∴$\frac{BP}{PC}$=$\frac{4}{3}$,
∴$\frac{{S}_{△APB}}{{S}_{△APC}}$=$\frac{4}{3}$,即$\frac{84+x+40}{30+35+y}$=$\frac{4}{3}$,
$\frac{{S}_{△BOC}}{{S}_{△QOC}}$=2,
∴OB=2OQ,
∴$\frac{{S}_{△ABO}}{{S}_{△AQO}}$=2,即$\frac{84+x}{y}$=2,
则$\left\{\begin{array}{l}{4y-3x=108}\\{2y-x=84}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=60}\\{y=72}\end{array}\right.$,
∴△ABC的面积为:40+30+35+84+60+72=321.
点评 本题开车的是三角形的面积计算,掌握两个三角形有一个相同的高,它们的面积之比等于相应的底之比是解题的关键.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案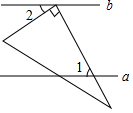 如图,直线a∥b,三角尺的直角顶点在直线b上,若∠1=50°,则∠2等于( )
如图,直线a∥b,三角尺的直角顶点在直线b上,若∠1=50°,则∠2等于( )| A. | 50° | B. | 40° | C. | 45° | D. | 25° |
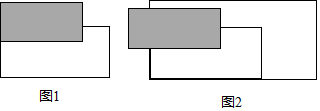
| A. | (m+a)(n+b) | B. | m(n+b)+a(n+b) | C. | mn+b(m+a)+a(n+b) | D. | mn+bm+an+ab |
 实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{a^2}$=b.
实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{a^2}$=b. 在平面直角坐标中,抛物线y=ax2+bx+3与x轴分别交于点A(2,0)、点B(点B在点A右侧),与y轴交于点C,tan∠CBA=$\frac{1}{2}$.
在平面直角坐标中,抛物线y=ax2+bx+3与x轴分别交于点A(2,0)、点B(点B在点A右侧),与y轴交于点C,tan∠CBA=$\frac{1}{2}$.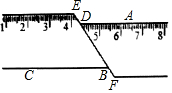 如图:一把直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠DBC=50°,则∠ADE的度数为130°.
如图:一把直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠DBC=50°,则∠ADE的度数为130°.