��Ŀ����
10����ֱ֪��l1��l2��ֱ��l3��ֱ��l1��l2���ڵ�C��D����P��ֱ��l3��һ����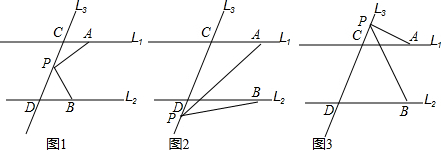
��1����ͼ1������P���߶�CD���˶�ʱ����PAC����APB����PBD֮�����ʲô������ϵ�����������۲�˵�����ɣ�
��2������P��C��D���������˶�ʱ��P�����C��D���غϣ���ͼ2��ͼ3����������1���еĽ����Ƿ�����������������ֱ��д����PAC����APB����PBD֮���������ϵ������д���ɣ�
���� ��1������P��PE��l1������ƽ���ߵ����ʼ��ɵõ�����APE=��PAC����BPE=��PBD�����ݡ�APE+��BPE=��PAC+��PBD���ɵá�APB=��PAC+��PBD��
��2�����ݣ�1���ķ���������P��PE��l1������ƽ���ߵ����ʣ��ɵá�APE=��PAC����PBD=��BPE��ͼ2�и��ݡ�APB=��APE-��BPE���ɵá�PAC=��APB+��PBD��ͼ3�У����ݡ�APB=��BPE-��APE���ɵá�PBD=��PAC+��APB��
��� �⣺��1����APB=��PAC+��PBD��
��ͼ1������P��PE��l1��
���APE=��PAC��
��l1��l2��
��PE��l2��
���BPE=��PBD��
���APE+��BPE=��PAC+��PBD��
���APB=��PAC+��PBD��
��2����������
��ͼ2����PAC=��APB+��PBD��
���ɣ�����P��PE��l1��
���APE=��PAC��
��l1��l2��
��PE��l2��
���BPE=��PBD��
�ߡ�APB=��APE-��BPE=��PAC-��PBD��
���PAC=��APB+��PBD��
��ͼ3����PBD=��PAC+��APB��
���ɣ�����P��PE��l1��
���APE=��PAC��
��l1��l2��
��PE��l2��
���BPE=��PBD��
��APB=��BPE-��APE=��PBD-��PAC��
���PBD=��PAC+��APB��
���� ������Ҫ������ƽ���ߵ����ʣ�����ʱע�⣺��ֱ��ƽ�У��ڴ�����ȣ��������Ĺؼ��ǹ���P��ƽ���ߣ������ڴ��ǣ�

 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�| A�� | 18�� | B�� | 36�� | C�� | 54�� | D�� | 72�� |
| A�� | ���a��b��b��c����ôa��c | B�� | ���a��b��b��c����ôa��c | ||
| C�� | ���a��b��b��c����ôa��c | D�� | ���a��b��a��c����ôb��c |
| A�� | ��a-b����a-b��=a2-b2 | B�� | ��x+2����x-2��=x2-2 | ||
| C�� | ��2x+1����2x-1��=2x2-1 | D�� | ��-3x+2����-3x-2��=9x2-4 |
 ʵ��a��b�������ϵĶ�Ӧ����ͼ��ʾ����|a-b|-$\sqrt{a^2}$=b��
ʵ��a��b�������ϵĶ�Ӧ����ͼ��ʾ����|a-b|-$\sqrt{a^2}$=b��