Question

6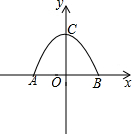．某小区的大门是如图所示的一个抛物线形状的门窗，门洞的高为4m，门洞地面的宽为6米，建立如图所示的平面直角坐标系，使抛物线的对称轴为y轴．
（1）求该抛物线的解析式；
（2）在一次小区活动中，要在该门洞上距离地面3米高的位置挂上一条水平的条幅，条幅的两端在抛物线上，求该条幅的长度．

Answer 1

分析 （1）根据A、B、C的坐标，用待定系数法即可求出过此三点的抛物线解析式；
（2）把y=3代入函数表达式解方程即可．

解答 解：（1）根据题意，A（-3，0），B（3，0），C（0，4），
设y=ax²+4，把A（-3，0）代入，
得9a+4=0，
解得：a=-$\frac{4}{9}$，
∴y=-$\frac{4}{9}$x²+4；
（2）把y=3代入y=-$\frac{4}{9}$x²+4，则
3=-$\frac{4}{9}$x²+4，
解得：x=±$\frac{3}{2}$，
$\frac{3}{2}-（-\frac{3}{2}）$=3，
所以该条幅的长度为3米．

点评 本题主要考查了二次函数的实际应用，求出函数表达式是解决问题的关键．