题目内容
16.已知(a-2)2+|b-1|=0;试求下式的值.$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+$\frac{1}{(a+3)(b+3)}$+…+$\frac{1}{(a+2013)(b+2013)}$=
分析 由非负数的性质可求得a=2,b=1,然后将a=2,b=1代入原式,然后再利用拆项裂项法求解即可.
解答 解:∵(a-2)2+|b-1|=0,
∴a-2=0,b-1=0.
∴a=2,b=1.
∴原式=$\frac{1}{2×3}+\frac{1}{3×4}+\frac{1}{4×5}+…+\frac{1}{2014×2015}$
=$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}$+…+$\frac{1}{2014}$-$\frac{1}{2015}$
=$\frac{1}{2}-\frac{1}{2015}$
=$\frac{2013}{4030}$.
点评 本题主要考查的是求代数式的值、非负数的性质,拆项裂项法的应用是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.二次函数y=x2-1的图象可由下列哪个函数图象向右平移1个单位,向下平移2个单位得到( )
| A. | y=(x-1)2+1 | B. | y=(x+1)2+1 | C. | y=(x-1)2-3 | D. | y=(x+1)2+3 |
8.如果$\sqrt{{a}^{2}}$有意义,则a的取值范围是( )
| A. | 有理数 | B. | 整数 | C. | 非负数 | D. | 任意实数 |
6.A,B是平面内的两个定点,在平面内找一点C,使△ABC构成等腰直角三角形,这样的C点可找( )
| A. | 2个 | B. | 4个 | C. | 6个 | D. | 8个 |
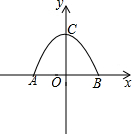 某小区的大门是如图所示的一个抛物线形状的门窗,门洞的高为4m,门洞地面的宽为6米,建立如图所示的平面直角坐标系,使抛物线的对称轴为y轴.
某小区的大门是如图所示的一个抛物线形状的门窗,门洞的高为4m,门洞地面的宽为6米,建立如图所示的平面直角坐标系,使抛物线的对称轴为y轴.