题目内容
2.化简:$\frac{x+2\sqrt{xy}+y}{\sqrt{x}+\sqrt{y}}$-$\frac{x\sqrt{x}-y\sqrt{y}}{x+\sqrt{xy}+y}$.分析 先把两个分式的分子利用完全平方公式和立方差公式因式分解,进一步约分化简,合并后得出答案即可.
解答 解:原式=$\frac{(\sqrt{x}+\sqrt{y})^{2}}{\sqrt{x}+\sqrt{y}}$-$\frac{(\sqrt{x}-\sqrt{y})(x+\sqrt{xy}+y)}{x+\sqrt{xy}+y}$
=$\sqrt{x}$+$\sqrt{y}$+$\sqrt{x}$-$\sqrt{y}$
=2$\sqrt{x}$.
点评 此题考查二次根式的化简,掌握完全平方公式和立方差公式因式分解是解决问题的关键.

练习册系列答案
相关题目
2.在△ABC中,已知a=3$\sqrt{3}$,b=2,∠C=150°,则c=( )
| A. | 49 | B. | 7 | C. | 13 | D. | $\sqrt{13}$ |
7.二次函数y=x2-1的图象可由下列哪个函数图象向右平移1个单位,向下平移2个单位得到( )
| A. | y=(x-1)2+1 | B. | y=(x+1)2+1 | C. | y=(x-1)2-3 | D. | y=(x+1)2+3 |
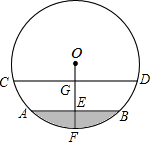 一根圆管的横截面积如图所示,圆管内原有积水的水面宽AB=40cm,水深EF=10cm,当水面上升10cm(即EG=10cm)时,水面的宽CD是多少(结果保留小数点后一位)
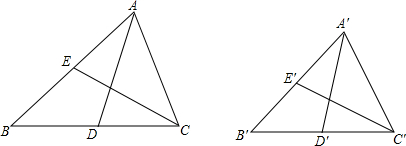
一根圆管的横截面积如图所示,圆管内原有积水的水面宽AB=40cm,水深EF=10cm,当水面上升10cm(即EG=10cm)时,水面的宽CD是多少(结果保留小数点后一位) 如图,在△ABC中,∠B=90°,∠BAC=∠C,ED⊥AC于点D,且DE=BE,求∠AED的度数.
如图,在△ABC中,∠B=90°,∠BAC=∠C,ED⊥AC于点D,且DE=BE,求∠AED的度数.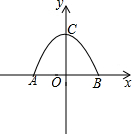 某小区的大门是如图所示的一个抛物线形状的门窗,门洞的高为4m,门洞地面的宽为6米,建立如图所示的平面直角坐标系,使抛物线的对称轴为y轴.
某小区的大门是如图所示的一个抛物线形状的门窗,门洞的高为4m,门洞地面的宽为6米,建立如图所示的平面直角坐标系,使抛物线的对称轴为y轴.