题目内容
1. 如图,AB∥CD,AD与BC交于点E,连接AC、BD,∠ABC=∠ADC.
如图,AB∥CD,AD与BC交于点E,连接AC、BD,∠ABC=∠ADC.写出图中的所有全等三角形,并对其中的一对全等三角形写出理由.
分析 由AB∥CD结合∠ABC=∠ADC,可求得∠ADC=∠DAB=∠ABC=∠BCD,可求得EA=EB、EC=ED,可求得AD=BC,可证明△ACD≌△BDC,同理可证明△ABC≌△BDA,进一步可证明△ACE≌△BDE.
解答 解:
全等三角形有:△ACD≌△BDC,△ABC≌△BDA和△ACE≌△BDE.
∵AB∥CD,
∴∠ADC=∠DAB,∠ABC=∠BCD,
∵∠ABC=∠ADC,
∴∠ADC=∠DAB=∠ABC=∠BCD,
∴EA=EB,EC=ED,
∴AD=BC,
在△ACD和△BDC中
$\left\{\begin{array}{l}{AD=BC}\\{∠ADC=∠BCD}\\{CD=DC}\end{array}\right.$
∴△ACD≌△BDC(SAS).
同理可证明△ACD≌△BDC、△ACE≌△BDE.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和性质(即全等三角形的对应边相等、对应角相等)是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=76°,∠DOF=90°,求∠EOF的度数.
如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=76°,∠DOF=90°,求∠EOF的度数.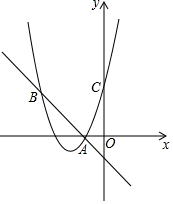 如图,已知二次函数y1=ax2+bx+c的图象经过点A(-1,0),C(0,3),且对称轴为直线x=-2,一次函数y2=mx+n的图象经过点A、B.
如图,已知二次函数y1=ax2+bx+c的图象经过点A(-1,0),C(0,3),且对称轴为直线x=-2,一次函数y2=mx+n的图象经过点A、B.