题目内容
12. 如图,在△ABC中,AB=BC,BO、CO分别平分∠ABC和∠ACB,过点O作DE∥BC,分别交边AB、AC于点D和点E,如果△ABC的周长等于14,△ADE的周长等于9,那么AC=4.
如图,在△ABC中,AB=BC,BO、CO分别平分∠ABC和∠ACB,过点O作DE∥BC,分别交边AB、AC于点D和点E,如果△ABC的周长等于14,△ADE的周长等于9,那么AC=4.
分析 由BO平分∠ABC,CO平分∠ACB,过点O作DE∥BC,易得△BOD与△COE是等腰三角形,又由△ADE的周长为9,可得AB+AC=9,又由△ABC的周长是14,即可求得答案.
解答 解:∵BO平分∠ABC,CO平分∠ACB,
∴∠ABO=∠OBC,∠ACO=∠OCB,
∵DE∥BC,
∴∠BOD=∠OBC,∠COE=∠OCB,
∴∠ABO=∠BOD,∠ACO=∠COE,
∴BD=OD,CE=OE,
∵△ADE的周长为9,
∴AD+DE+AE=AD+OD+OE+AE=AD+BD+CE+AE=AB+AC=9,
∵△ABC的周长是14,
∴AB+AC+BC=14,
∵AB=BC,
∴2AB+AC=14,
∴AC=4.
故答案为:4.
点评 此题考查了等腰三角形的性质与判定,角平分线的性质,平行线的性质,三角形的周长,弄清△ADE的周长和△ABC的周长之间的关系是解题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
2.一组数据1、2、2、3、4、5、6的中位数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°
如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30° 如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=215°.
如图,在⊙O的内接五边形ABCDE中,∠CAD=35°,则∠B+∠E=215°.
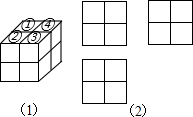 如图,用八个同样大小的小立方体搭成一个大立方体,小明从如图(1)上面的四个小立方体(①②③④)中取走了任意两个后,得到的新几何体的三视图如图(2)所示的概率为$\frac{1}{3}$.
如图,用八个同样大小的小立方体搭成一个大立方体,小明从如图(1)上面的四个小立方体(①②③④)中取走了任意两个后,得到的新几何体的三视图如图(2)所示的概率为$\frac{1}{3}$.