题目内容
17．计算：$\sqrt{12}-{（{π-\sqrt{2015}}）^0}+{（{-\frac{1}{3}}）^{-2}}$-4sin60°．分析 原式第一项化为最简二次根式，第二项利用零指数幂法则计算，第三项利用负整数指数幂法则计算，最后一项利用特殊角的三角函数值计算即可得到结果．
解答 解：原式=2$\sqrt{3}$-1+9-4×$\frac{\sqrt{3}}{2}$
=8．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
5．
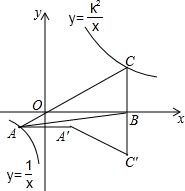如图，已知在平面直角坐标系xOy中，O是坐标原点，点A是函数y=$\frac{1}{x}$（x＜0）图象上一点，AO的延长线交函数y=$\frac{{k}^{2}}{x}$（x＞0，k是不等于0的常数）的图象于点C，点A关于y轴的对称点为A′，点C关于x轴的对称点为C′，交于x轴于点B，连结AB，AA′，A′C′．若△ABC的面积等于6，则由线段AC，CC′，C′A′，A′A所围成的图形的面积等于（ ）
如图，已知在平面直角坐标系xOy中，O是坐标原点，点A是函数y=$\frac{1}{x}$（x＜0）图象上一点，AO的延长线交函数y=$\frac{{k}^{2}}{x}$（x＞0，k是不等于0的常数）的图象于点C，点A关于y轴的对称点为A′，点C关于x轴的对称点为C′，交于x轴于点B，连结AB，AA′，A′C′．若△ABC的面积等于6，则由线段AC，CC′，C′A′，A′A所围成的图形的面积等于（ ）| A． | 8 | B． | 10 | C． | 3$\sqrt{10}$ | D． | 4$\sqrt{6}$ |
如图，在△ABC中，AB=BC，BO、CO分别平分∠ABC和∠ACB，过点O作DE∥BC，分别交边AB、AC于点D和点E，如果△ABC的周长等于14，△ADE的周长等于9，那么AC=4．
2．事件A：“若a是实数，则|a|≥a”；事件B：“若实数x满足x＞-x，则x正实数”．则下列关于事件A和事件B的说法正确的是（ ）
| A． | 事件A是必然事件，而事件B是随机事件 | |
| B． | 事件A是随机事件，而事件B是必然事件 | |
| C． | 事件A是必然事件，而事件B是必然事件 | |
| D． | 事件A是随机事件，而事件B是随机事件 |
7．
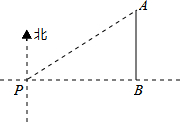如图，一艘海轮位于灯塔P的北偏东55°方向，距离灯塔2海里的点A处，如果海轮沿正南方向航行到灯塔的正东方向，海轮航行的距离AB长是（ ）
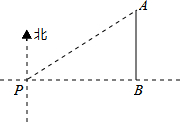如图，一艘海轮位于灯塔P的北偏东55°方向，距离灯塔2海里的点A处，如果海轮沿正南方向航行到灯塔的正东方向，海轮航行的距离AB长是（ ）| A． | 2海里 | B． | 2sin55°海里 | C． | 2cos55°海里 | D． | 2tan55°海里 |