��Ŀ����
20���������x��һԪ���η���ax2+bx+c=0������ʵ������������һ����Ϊ��һ������2������������ķ���Ϊ���������̡������¹��ڱ������̵�˵������ȷ���Ǣڢۣ�д��������ȷ˵������ţ��ٷ���x2-x-2=0�DZ������̣�
������x-2����mx+n��=0�DZ������̣���4m2+5mn+n2=0��
�����㣨p��q���ڷ���������y=$\frac{2}{x}$��ͼ���ϣ������x�ķ���px2+3x+q=0�DZ������̣�
��������ax2+bx+c=0�DZ������̣�����������M��1+t��s����N��4-t��s������������y=ax2+bx+c�ϣ���ax2+bx+c=0��һ����Ϊ$\frac{5}{4}$��
���� �ٽⷽ��x2-x-2=0�ã�x1=2��x2=-1���õ�����x2-x-2=0���DZ������̣��ʢٴ����ɣ�x-2����mx+n��=0�DZ������̣���x1=2��x2=-$\frac{n}{m}$���õ�$\frac{n}{m}$=-1����$\frac{n}{m}$=-4����m+n=0��4m+n=0���ǵõ�4m2+5mn+n2=��4m+n����m+n��=0���ʢ���ȷ�����ɵ㣨p��q���ڷ���������y=$\frac{2}{x}$��ͼ���ϣ��õ�pq=2���ⷽ��px2+3x+q=0�ã�x1=-$\frac{1}{p}$��x2=-$\frac{2}{p}$���ʡ����ȷ�����ɷ���ax2+bx+c=0�DZ������̣��õ�x1=2x2������������M��1+t��s����N��4-t��s������������y=ax2+bx+c�ϣ���
�õ������ߵĶԳ���x=$\frac{{x}_{1}{+x}_{2}}{2}$=$\frac{1+t+4-t}{2}$=$\frac{5}{2}$���������x1=$\frac{5}{3}$���ʢܴ���
��� �⣺�ٽⷽ��x2-x-2=0�ã�x1=2��x2=-1��
���x2-x-2=0���DZ������̣��ʢٴ���
�ڡߣ�x-2����mx+n��=0�DZ������̣���x1=2��x2=-$\frac{n}{m}$��
��$\frac{n}{m}$=-1����$\frac{n}{m}$=-4��
��m+n=0��4m+n=0��
��4m2+5mn+n2=��4m+n����m+n��=0���ʢ���ȷ��
�ۡߵ㣨p��q���ڷ���������y=$\frac{2}{x}$��ͼ���ϣ�
��pq=2��
�ⷽ��px2+3x+q=0�ã�x1=-$\frac{1}{p}$��x2=-$\frac{2}{p}$��
��x2=2x1���ʢ���ȷ��
�ܡ߷���ax2+bx+c=0�DZ������̣�
����x1=2x2��
����������M��1+t��s����N��4-t��s������������y=ax2+bx+c�ϣ�
�������ߵĶԳ���x=$\frac{{x}_{1}{+x}_{2}}{2}$=$\frac{1+t+4-t}{2}$=$\frac{5}{2}$��
��x1+x2=5��
��x2+2x2=5��
��x2=$\frac{5}{3}$���ʢܴ���
�ʴ�Ϊ���ڢۣ�
���� ���⿼���˸���ϵ���Ĺ�ϵ�������б�ʽ������������ͼ���ϵ���������������κ���ͼ���ϵ��������������ȷ�����⡰�������̡��Ķ����ǽ���Ĺؼ���

| A�� | 26��104ƽ���� | B�� | 2.6��104ƽ���� | C�� | 2.6��105ƽ���� | D�� | 2.6��106ƽ���� |
| A�� | 720�� | B�� | 1080�� | C�� | 1440�� | D�� | 1880�� |
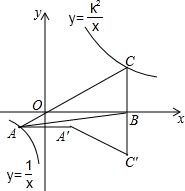 ��ͼ����֪��ƽ��ֱ������ϵxOy�У�O������ԭ�㣬��A�Ǻ���y=$\frac{1}{x}$��x��0��ͼ����һ�㣬AO���ӳ��߽�����y=$\frac{{k}^{2}}{x}$��x��0��k�Dz�����0�ij�������ͼ���ڵ�C����A����y��ĶԳƵ�ΪA�䣬��C����x��ĶԳƵ�ΪC�䣬����x���ڵ�B������AB��AA�䣬A��C�䣮����ABC���������6�������߶�AC��CC�䣬C��A�䣬A��A��Χ�ɵ�ͼ�ε�������ڣ�������
��ͼ����֪��ƽ��ֱ������ϵxOy�У�O������ԭ�㣬��A�Ǻ���y=$\frac{1}{x}$��x��0��ͼ����һ�㣬AO���ӳ��߽�����y=$\frac{{k}^{2}}{x}$��x��0��k�Dz�����0�ij�������ͼ���ڵ�C����A����y��ĶԳƵ�ΪA�䣬��C����x��ĶԳƵ�ΪC�䣬����x���ڵ�B������AB��AA�䣬A��C�䣮����ABC���������6�������߶�AC��CC�䣬C��A�䣬A��A��Χ�ɵ�ͼ�ε�������ڣ�������| A�� | 8 | B�� | 10 | C�� | 3$\sqrt{10}$ | D�� | 4$\sqrt{6}$ |
| A�� | x2=2 | B�� | x2-��k+1��x+��k+1��=0 | C�� | 2x2-$\sqrt{2}$x+1=0 | D�� | 1+$\frac{x}{x-1}$=$\frac{1}{x-1}$ |
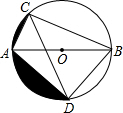 ��ͼ��ABΪ��O��ֱ������AC=3����ABC=30�㣬��ACB��ƽ���߽���O�ڵ�D��
��ͼ��ABΪ��O��ֱ������AC=3����ABC=30�㣬��ACB��ƽ���߽���O�ڵ�D�� ��ͼ���ڡ�ABC�У�AB=BC��BO��CO�ֱ�ƽ�֡�ABC�͡�ACB������O��DE��BC���ֱ�AB��AC�ڵ�D�͵�E�������ABC���ܳ�����14����ADE���ܳ�����9����ôAC=4��
��ͼ���ڡ�ABC�У�AB=BC��BO��CO�ֱ�ƽ�֡�ABC�͡�ACB������O��DE��BC���ֱ�AB��AC�ڵ�D�͵�E�������ABC���ܳ�����14����ADE���ܳ�����9����ôAC=4��