题目内容
20.解方程组$\left\{\begin{array}{l}{\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1}\\{y=x-3}\end{array}\right.$.分析 把②代入①得到关于x的一元二次方程,解方程求出x的值,把x的值代入②求出y的值即可.
解答 解:$\left\{\begin{array}{l}{\frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1①}\\{y=x-3②}\end{array}\right.$,
把②代入①得,
$\frac{{x}^{2}}{5}+\frac{({x-3)}^{2}}{4}=1$,
整理得,9x2-30x+25=0,
解得,x1=x2=$\frac{5}{3}$,
把x=$\frac{5}{3}$代入②得,y=-$\frac{4}{3}$,
所以方程组的解为:$\left\{\begin{array}{l}{x=\frac{5}{3}}\\{y=-\frac{4}{3}}\end{array}\right.$.
点评 本题考查的是代入消元法解高次方程,掌握代入消元法的一般步骤:先消去一个未知数,再解关于另一个未知数的一元二次方程,把求得结果代入一个较简单的方程中是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
 如图,已知∠EBF,用下面的方法可把它两等分:
如图,已知∠EBF,用下面的方法可把它两等分: 如图,在正方形ABCD和正方形CEFG中,点D在CG边上,BC=$\sqrt{2}$,CE=3$\sqrt{2}$,若H是AF的中点,则CH的长为$\sqrt{10}$.
如图,在正方形ABCD和正方形CEFG中,点D在CG边上,BC=$\sqrt{2}$,CE=3$\sqrt{2}$,若H是AF的中点,则CH的长为$\sqrt{10}$. 如图,CE是△ABC的外角∠ACD的平分线,且CE交CA的延长线于E,求证:∠BAC=∠B+2∠E.
如图,CE是△ABC的外角∠ACD的平分线,且CE交CA的延长线于E,求证:∠BAC=∠B+2∠E.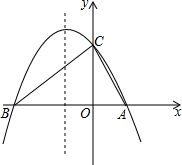 如图,抛物线与x轴交于A(2,0)、B两点,与y轴的交点为C(0,3),它的对称轴是直线x=-$\frac{1}{2}$
如图,抛物线与x轴交于A(2,0)、B两点,与y轴的交点为C(0,3),它的对称轴是直线x=-$\frac{1}{2}$
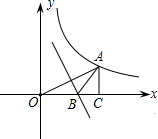 如图,已知点A在双曲线y=$\frac{6}{x}$上,且OA=4,过A作AC⊥x轴于C,OA的垂直平分线交OC于B,则△AOC的面积为3.
如图,已知点A在双曲线y=$\frac{6}{x}$上,且OA=4,过A作AC⊥x轴于C,OA的垂直平分线交OC于B,则△AOC的面积为3.