题目内容
5.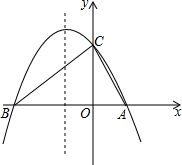 如图,抛物线与x轴交于A(2,0)、B两点,与y轴的交点为C(0,3),它的对称轴是直线x=-$\frac{1}{2}$
如图,抛物线与x轴交于A(2,0)、B两点,与y轴的交点为C(0,3),它的对称轴是直线x=-$\frac{1}{2}$(1)求抛物线的函数解析式;
(2)求△ABC的面积.
分析 (1)利用抛物线的对称性先确定B(-3,0),则可设交点式y=a(x+3)(x-2),然后把C点坐标代入求出a即可;
(2)利用三角形面积公式求解.
解答 解:(1)∵抛物线的对称轴是直线x=-$\frac{1}{2}$,
而A(2,0),
∴B(-3,0),
设抛物线解析式为y=a(x+3)(x-2),
把C(0,3)代入得a•3•(-2)=3,解得a=-$\frac{1}{2}$,
∴抛物线解析式为y=-$\frac{1}{2}$(x+3)(x-2),即y=-$\frac{1}{2}$x2-$\frac{1}{2}$x-3;
(2)S△ABC=$\frac{1}{2}$×(2+3)×3=$\frac{15}{2}$.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数.解决此类问题的关键是把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为求方程ax2+bx+c=0的解的问题.也考查了待定系数法求抛物线解析式.

练习册系列答案
相关题目
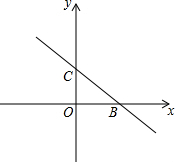 如图,已知直线y=-$\frac{2}{3}$x+2与x轴、y轴分别相交于点B、点C
如图,已知直线y=-$\frac{2}{3}$x+2与x轴、y轴分别相交于点B、点C
 在图中的四个图形中,只有一个是由左边的纸板折叠而成的,这个图形是( )
在图中的四个图形中,只有一个是由左边的纸板折叠而成的,这个图形是( )



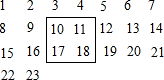 把正整数1,2,3,4,5,6,7…按如图方式排列成一个“数阵”.
把正整数1,2,3,4,5,6,7…按如图方式排列成一个“数阵”.
 如图,一个高8cm圆锥形零件,底面圆直径12cm,此圆锥的侧面积是60πcm2(结果保留π).
如图,一个高8cm圆锥形零件,底面圆直径12cm,此圆锥的侧面积是60πcm2(结果保留π).