题目内容
1．若xm=9，xn=6．xk=4．则xm-2n+2k的值为（ ）| A． | 0 | B． | 1 | C． | 4 | D． | 8 |
分析 根据幂的乘方，可得同底数幂的乘除法，根据同底数幂的乘法底数不变指数相加，同底数幂的除法底数不变指数相减，可得答案．
解答 解：x2n=（xn）2=36，
x2k=（xk）2=16．
xm-2n+2k=xm÷x2n×x2k=9÷36×16=4，
故选：C．
点评 本题考查了同底数幂的除法，熟记法则并根据法则计算是解题关键．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
11．
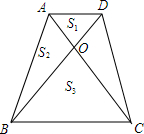如下图，梯形ABCD中，AD∥BC，AC与BD交于O，记△AOD、△ABO、△BOC的面积分别为S1、S2、S3，则S1+S3与2S2的大小关系为（ ）
如下图，梯形ABCD中，AD∥BC，AC与BD交于O，记△AOD、△ABO、△BOC的面积分别为S1、S2、S3，则S1+S3与2S2的大小关系为（ ）| A． | 无法确定 | B． | S1+S3＜2S2 | C． | S1+S3=2S2 | D． | S1+S3＞2S2 |
9．已知一元二次方程ax2+c=0（a≠0），若方程有解，则必须有c等于（ ）
| A． | -$\frac{1}{2}$ | B． | -1 | C． | $\frac{1}{2}$ | D． | 不能确定 |
如图，AB∥CD，点P为CD上一点，∠EBA、∠EPC的角平分线交于点F，已知∠F=42°，则∠E=82度．