题目内容
11.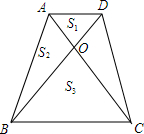 如下图,梯形ABCD中,AD∥BC,AC与BD交于O,记△AOD、△ABO、△BOC的面积分别为S1、S2、S3,则S1+S3与2S2的大小关系为( )
如下图,梯形ABCD中,AD∥BC,AC与BD交于O,记△AOD、△ABO、△BOC的面积分别为S1、S2、S3,则S1+S3与2S2的大小关系为( )| A. | 无法确定 | B. | S1+S3<2S2 | C. | S1+S3=2S2 | D. | S1+S3>2S2 |
分析 根据AD∥BC,得到△AOD∽△COB,根据相似三角形的性质得到$\frac{OD}{BO}=\frac{OA}{OC}$=$\frac{a}{b}$,由于△AOD与△AOB等高,于是得到S1:S2=AD:BC=a:b,求得S1=$\frac{a}{b}$S2,S3=$\frac{b}{a}$S2,证得S1+S3=($\frac{a}{b}$+$\frac{b}{a}$)S2=$\frac{{a}^{2}+{b}^{2}}{ab}$S2,根据非负数的定义得到a2+b2>2ab,于是得到结论.
解答 解:∵AD∥BC,
∴△AOD∽△COB,
∴$\frac{OD}{BO}=\frac{OA}{OC}$=$\frac{a}{b}$,
∵△AOD与△AOB等高,
∴S1:S2=AD:BC=a:b,
∴S1=$\frac{a}{b}$S2,S3=$\frac{b}{a}$S2,
∴S1+S3=($\frac{a}{b}$+$\frac{b}{a}$)S2=$\frac{{a}^{2}+{b}^{2}}{ab}$S2,
∵a≠b,
∴a2+b2>2ab,
∴$\frac{{a}^{2}+{b}^{2}}{ab}$>2,
∴S1+S3>2S2,
故选D.
点评 本题考查了相似三角形的判定和性质,梯形的性质,非负数的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
则当y<5时,x的取值范围为( )
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | … |
| A. | 0<x<4 | B. | -4<x<4 | C. | x<-4或x>4 | D. | x>4 |
2.方程3x(2x-4)=0的解是( )
| A. | x=3 | B. | x=2 | C. | x=0 | D. | x1=0,x2=2 |
16.若二次函数y=x2+bx-5的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为( )
| A. | x1=0,x2=4 | B. | x1=1,x2=5 | C. | x1=1,x2=-5 | D. | x1=-1,x2=5 |
20.下列各式中,不能用平方差公式的是( )
| A. | (4x-3y)(3y-4x) | B. | (-4x+3y)(4x+3y) | C. | (-4x+3y)(-4x-3y) | D. | (4x+3y)(4x-3y) |
1.若xm=9,xn=6.xk=4.则xm-2n+2k的值为( )
| A. | 0 | B. | 1 | C. | 4 | D. | 8 |
 如图,在△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交 AC于点F.BE=4,CF=3,则EF=7.
如图,在△ABC中,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交 AC于点F.BE=4,CF=3,则EF=7.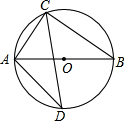 己知:在⊙O中,直径AB的长为10cm,弦AC的长为6cm,∠ACB的平分线交⊙O于点D,
己知:在⊙O中,直径AB的长为10cm,弦AC的长为6cm,∠ACB的平分线交⊙O于点D,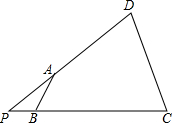 如图,四边形ABCD中,∠ABC=∠DCB,DA,CB的延长线交于点P.
如图,四边形ABCD中,∠ABC=∠DCB,DA,CB的延长线交于点P.