题目内容
17. 如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线交于点F,已知∠F=42°,则∠E=82度.
如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线交于点F,已知∠F=42°,则∠E=82度.
分析 设∠EPC=2x,∠EBA=2y,根据角平分线的性质得到∠CPF=∠EPF=x,∠EBF=∠FBA=y,根据外角的性质得到∠1=∠F+∠ABF=42°+y,∠2=∠EBA+∠E=2y+∠E,由平行线的性质得到∠1=∠CPF=x,∠2=∠EPC=2x,于是得到方程2y+∠E=2(42°+y),即可得到结论.
解答  解:设∠EPC=2x,∠EBA=2y,
解:设∠EPC=2x,∠EBA=2y,
∵∠EBA、∠EPC的角平分线交于点F,
∴∠CPF=∠EPF=x,∠EBF=∠FBA=y,
∵∠1=∠F+∠ABF=42°+y,
∠2=∠EBA+∠E=2y+∠E,
∵AB∥CD,
∴∠1=∠CPF=x,∠2=∠EPC=2x,
∴∠2=2∠1,
∴2y+∠E=2(42°+y),
∴∠E=82°.
故答案为:82.
点评 本题考查了平行线的性质以及三角形的外角的性质:三角形的外角等于两个不相邻的内角的和,正确设未知数是关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
1.若xm=9,xn=6.xk=4.则xm-2n+2k的值为( )
| A. | 0 | B. | 1 | C. | 4 | D. | 8 |
5.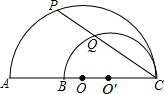 如图,AC、BC是两个半圆的直径,∠ACP=30°,AB=10cm,则PQ长为( )
如图,AC、BC是两个半圆的直径,∠ACP=30°,AB=10cm,则PQ长为( )
 如图,AC、BC是两个半圆的直径,∠ACP=30°,AB=10cm,则PQ长为( )
如图,AC、BC是两个半圆的直径,∠ACP=30°,AB=10cm,则PQ长为( )| A. | 5cm | B. | 5$\sqrt{3}$cm | C. | 6cm | D. | 8cm |
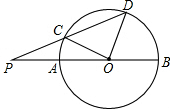 如图,已知直径BA与弦DC的延长线交于点P,且PC=CO,$\widehat{CD}$=$\widehat{AC}$+$\widehat{DB}$,求∠DOB的度数.
如图,已知直径BA与弦DC的延长线交于点P,且PC=CO,$\widehat{CD}$=$\widehat{AC}$+$\widehat{DB}$,求∠DOB的度数. 画出以下几何体的三视图.
画出以下几何体的三视图.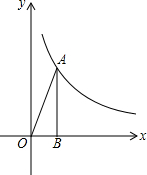 如图,点A(2,m)在双曲线y=$\frac{k}{x}$上,AB⊥x轴,B为垂足,tan∠AOB=2.
如图,点A(2,m)在双曲线y=$\frac{k}{x}$上,AB⊥x轴,B为垂足,tan∠AOB=2. 如图,AD∥BE,BD∥CE.
如图,AD∥BE,BD∥CE.