题目内容
7. 如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=6,CD=1,则EC的长为$\sqrt{73}$.
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=6,CD=1,则EC的长为$\sqrt{73}$.
分析 首先连接BE,由⊙O的半径OD⊥弦AB于点C,AB=6,CD=1,根据垂径定理可求得AC=BC=3,然后设OA=x,利用勾股定理可得方程:32+(x-1)2=x2,则可求得半径的长,继而利用三角形中位线的性质,求得BE的长,又由AE是直径,可得∠B=90°,继而求得答案.
解答 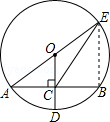 解:连接BE,
解:连接BE,
∵⊙O的半径OD⊥弦AB于点C,AB=6,
∴AC=BC=3,
设OA=x,
∵CD=1,
∴OC=x-1,
在Rt△AOC中,AC2+OC2=OA2,
∴32+(x-1)2=x2,
解得:x=5,
∴OA=OE=5,OC=4,
∴BE=2OC=8,
∵AE是直径,
∴∠B=90°,
∴CE=$\sqrt{B{C}^{2}+B{E}^{2}}$=$\sqrt{73}$.
故答案为:$\sqrt{73}$.
点评 此题考查了圆周角定理、垂径定理、勾股定理以及三角形中位线的性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
15.下列命题的逆命题是正确的是( )
| A. | 若a=b,则a2=b2 | B. | 若a>0,b>0,则ab>0 | ||
| C. | 等边三角形是锐角三角形 | D. | 全等三角形的对应边相等 |
16.甲、乙、丙、丁四位同学到木工厂参观时,木工师傅拿尺子要他们帮助检测一个窗框是否是矩形,他们各自做了如下检测,检测后,他们都说窗框是矩形,你认为正确的是( )
| A. | 甲量得窗框两组对边分别相等 | |
| B. | 乙量得窗框对角线相等 | |
| C. | 丙量得窗框的一组邻边相等 | |
| D. | 丁量得窗框的两组对边分别相等且两条对角线相等 |

 已知小正方形的边长为2厘米,大正方形的边长为4厘米,起始状态如图所示,大正方形固定不动,把小正方形以1厘米∕秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.完成下列问题:
已知小正方形的边长为2厘米,大正方形的边长为4厘米,起始状态如图所示,大正方形固定不动,把小正方形以1厘米∕秒的速度向右沿直线平移,设平移的时间为t秒,两个正方形重叠部分的面积为S平方厘米.完成下列问题: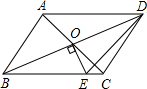 如图,?ABCD,对角线AC、BD交于点O,EO⊥BD于O交BC于E,若AB=5,△DEC的周长为13,则AD的长为8.
如图,?ABCD,对角线AC、BD交于点O,EO⊥BD于O交BC于E,若AB=5,△DEC的周长为13,则AD的长为8. 如图,四边形ABCD是菱形,边长为10cm,对角线AC,BD交于O,∠BAD=60°.
如图,四边形ABCD是菱形,边长为10cm,对角线AC,BD交于O,∠BAD=60°.