��Ŀ����
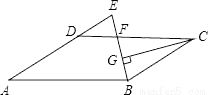
��ͼ����?ABCD�У�AB=12��AD=8����ABC��ƽ���߽�CD�ڵ�F����AD���ӳ����ڵ�E��CG��BE������ΪG����EF=2�����߶�CG�ij�Ϊ��������
A. 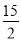 B.
B. 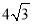 C.
C. 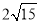 D.
D. 
 C
���������ߡ�ABC��ƽ���߽�CD�ڵ�F��
���ABE=��CBE��
���ı���ABCD��ƽ���ı��Σ�
��DC��AB��
���CBE=��CFB=��ABE=��E��
��CF=BC=AD=8��AE=AB=12��
��AD=8��
��DE=4��
��DC��AB��
�࣬
�࣬
��EB=6��
��CF=CB��CG��BF��
��BG=BF=2...
C
���������ߡ�ABC��ƽ���߽�CD�ڵ�F��
���ABE=��CBE��
���ı���ABCD��ƽ���ı��Σ�
��DC��AB��
���CBE=��CFB=��ABE=��E��
��CF=BC=AD=8��AE=AB=12��
��AD=8��
��DE=4��
��DC��AB��
�࣬
�࣬
��EB=6��
��CF=CB��CG��BF��
��BG=BF=2...
��ͼ1���ı���ABCD�У�AD��BC����ABC=��DCB��AB=DC��
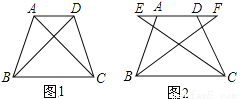
��1����֤��AC=DB��
��2����ͼ2��E��F����ͬʱ��A��D������ֱ��AD������ͬ���ٶȷ�����У�BF��CE���������֤����Ľ��ۡ�
 ��1��֤����������2��BF=CE
�����������������
��1���ɡ�ABC=��DCB��AB=DC���BC=CB����֤�ã���ABC�ա�DCB���Ӷ��ɵ�AC=DB��
��2��������ɵ�AE=DF���Ӷ��ɵ�AF=DE����AD��BC��ϡ�ABC=��DCB���á�BAD=��CDA���ٽ��AB=DC����֤�á�BAF�ա�CDE���Ӷ��ɵ�BF=CE.
���������
��1���ڡ�ABC�͡�DCB...
��1��֤����������2��BF=CE
�����������������
��1���ɡ�ABC=��DCB��AB=DC���BC=CB����֤�ã���ABC�ա�DCB���Ӷ��ɵ�AC=DB��
��2��������ɵ�AE=DF���Ӷ��ɵ�AF=DE����AD��BC��ϡ�ABC=��DCB���á�BAD=��CDA���ٽ��AB=DC����֤�á�BAF�ա�CDE���Ӷ��ɵ�BF=CE.
���������
��1���ڡ�ABC�͡�DCB... �������ʽ��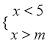 �н⣬��ôm��ȡֵ��Χ�ǣ�������
�н⣬��ôm��ȡֵ��Χ�ǣ�������
A. m��5 B. m��5 C. m��5 D. m��8
 C
���������߲���ʽ���н⣬
��m��5��
��ѡ��C��
C
���������߲���ʽ���н⣬
��m��5��
��ѡ��C�� ��֪ƽ���ı���ABCD�У�CEƽ�֡�BCD�ҽ�AD�ڵ�E��AF��CE���ҽ�BC�ڵ�F��
��1����֤����ABF�ա�CDE��
��2����ͼ������1=65�㣬���B�Ĵ�С��
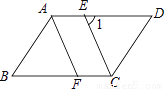
 ��1��֤������������2��50�㣮
�������������������1����ƽ���ı��ε����ʵó�AB=CD��AD��BC����B=��D���ó���1=��DCE��֤����AFB=��1����AAS֤����ABF�ա�CDE���ɣ���2���ɣ�1���á�1=��DCE=65�㣬��ƽ���ı��ε����ʺ��������ڽǺͶ������ɵó������
�����������1�����ı���ABCD��ƽ���ı��Σ� ��AB=CD��AD��BC����B=��D�� ���1=��DCE...
��1��֤������������2��50�㣮
�������������������1����ƽ���ı��ε����ʵó�AB=CD��AD��BC����B=��D���ó���1=��DCE��֤����AFB=��1����AAS֤����ABF�ա�CDE���ɣ���2���ɣ�1���á�1=��DCE=65�㣬��ƽ���ı��ε����ʺ��������ڽǺͶ������ɵó������
�����������1�����ı���ABCD��ƽ���ı��Σ� ��AB=CD��AD��BC����B=��D�� ���1=��DCE... ��ͼ���ڡ�ABC�У���D��E�ֱ��DZ�AB��AC���е㣬AF��BC������Ϊ��F����ADE=30�㣬DF=4����BF�ij�Ϊ�� ��
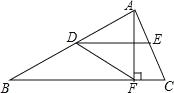
A��4 B��8 C��2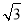 D��4
D��4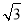
 D��
��������
�����������RT��ABF�У���AFB=90�㣬AD=DB��DF=4������ֱ��������б���������ʿɵ�AB=2DF=8������AD=DB��AE=EC���ɵ�DE��BC����ADE=��ABF=30�㣬����AF=AB=4���ɹ��ɶ����ɵ�BF=4����ѡD��
D��
��������
�����������RT��ABF�У���AFB=90�㣬AD=DB��DF=4������ֱ��������б���������ʿɵ�AB=2DF=8������AD=DB��AE=EC���ɵ�DE��BC����ADE=��ABF=30�㣬����AF=AB=4���ɹ��ɶ����ɵ�BF=4����ѡD�� ��ͼ���ڡ�ABC�У�AB=4��BC=6��DE��DF�ǡ�ABC����λ�ߣ����ı���BEDF���ܳ��ǣ� ��

A��5 B��7 C��8 D��10
 D��
��������
�����������AB=4��BC=6��DE��DF�ǡ�ABC����λ�ߣ���DE=AB=2��DF=BC=3��DE��BF��DF��BE�����ı���BEDFΪƽ���ı��Σ����ı���BEDF���ܳ�Ϊ��2��2+3��2=10����ѡD��
D��
��������
�����������AB=4��BC=6��DE��DF�ǡ�ABC����λ�ߣ���DE=AB=2��DF=BC=3��DE��BF��DF��BE�����ı���BEDFΪƽ���ı��Σ����ı���BEDF���ܳ�Ϊ��2��2+3��2=10����ѡD�� ��֪����ͼ�����ı���ABCD�У�AB��CD��E��BC���е㣬ֱ��AE��DC���ӳ����ڵ�F�����ж��ı���ABFC����״����֤����Ľ��ۣ�
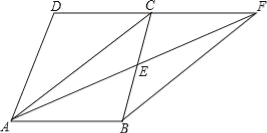
 �ı���ABFC��ƽ���ı��Σ�֤��������.
��������
�����������֤��ABE�ա�FCE��AAS����Ȼ������һ��Ա�ƽ������ȿ��ж��ı���ABFC��ƽ���ı���.
����������ı���ABFC��ƽ���ı��Σ��������£���AB��CD�����BAE=��CFE����E��BC���е㣬
��BE=CE���ڡ�ABE�͡�FCE�У������ABE�ա�FCE��AAS������AB=CF���֡�AB��CF�����ı���AB...
�ı���ABFC��ƽ���ı��Σ�֤��������.
��������
�����������֤��ABE�ա�FCE��AAS����Ȼ������һ��Ա�ƽ������ȿ��ж��ı���ABFC��ƽ���ı���.
����������ı���ABFC��ƽ���ı��Σ��������£���AB��CD�����BAE=��CFE����E��BC���е㣬
��BE=CE���ڡ�ABE�͡�FCE�У������ABE�ա�FCE��AAS������AB=CF���֡�AB��CF�����ı���AB... ��?ABCD�У�AB=3��BC=4����?ABCD��������ʱ�����н�����ȷ���У�������
��AC=5���ڡ�A+��C=180�㣻��AC��BD����AC=BD��
A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �٢ۢ�
 B
����������������ã���?ABCD��������ʱ���ı���ABCDΪ���Σ�
���A=��B=��C=��D=90�㣬AC=BD��
��AC==5��
����ȷ������ȷ������ȷ���۲���ȷ��
��ѡ��B��
B
����������������ã���?ABCD��������ʱ���ı���ABCDΪ���Σ�
���A=��B=��C=��D=90�㣬AC=BD��
��AC==5��
����ȷ������ȷ������ȷ���۲���ȷ��
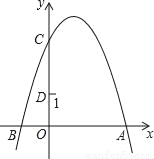
��ѡ��B�� ��ͼ��������y=��x2+2x+3��y�ύ�ڵ�C����D��0��1������P���������ϵĶ��㣮����PCD����CDΪ�ĵ��������Σ����P������Ϊ�� ����
 ��1+��2����1����2����
����������������
�ߡ�PCD����CDΪ�ĵ��������Σ����P���߶�CD�Ĵ�ֱƽ�����ϣ���ͼ����P��PE��y���ڵ�E����EΪ�߶�CD���е㣬����������y�ύ�ڵ�C����C��0��3������D��0��1������E������Ϊ��0��2������P��������Ϊ2�����У���y=2���ɵã����x=����P������Ϊ����2����2�����ʴ�Ϊ������2����2����
��1+��2����1����2����
����������������
�ߡ�PCD����CDΪ�ĵ��������Σ����P���߶�CD�Ĵ�ֱƽ�����ϣ���ͼ����P��PE��y���ڵ�E����EΪ�߶�CD���е㣬����������y�ύ�ڵ�C����C��0��3������D��0��1������E������Ϊ��0��2������P��������Ϊ2�����У���y=2���ɵã����x=����P������Ϊ����2����2�����ʴ�Ϊ������2����2���� 
