题目内容
14.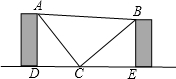 一个等腰直角三角板如图搁置在两柜之间,且点D,C,E在同一直线上,已知稍高的柜高AD为80cm,两柜距离DE为140cm.求稍矮的柜高BE.
一个等腰直角三角板如图搁置在两柜之间,且点D,C,E在同一直线上,已知稍高的柜高AD为80cm,两柜距离DE为140cm.求稍矮的柜高BE.
分析 首先证明△ADC≌△CEB,根据全等三角形的性质可得AD=CE,DC=BE,进而可得CE的长,然后可得DC的长度,从而求出BE长.
解答 解:由题意得:∠ADC=∠ACB=∠BEC=90°,AC=BC,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵∠BEC=90°,
∴∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中,$\left\{\begin{array}{l}{∠ADC=∠BEC}\\{∠ACD=∠CBE}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△CEB(AAS),
∴AD=CE,DC=BE,
∵AD=80cm,
∴CE=80cm,
∵DE=140cm,
∴DC=60cm,
∴BE=60cm.
点评 此题主要考查了全等三角形的应用,关键是掌握全等三角形的判定定理:SSS、SAS、ASA、AAS、HL.

练习册系列答案
相关题目
3.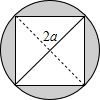 如图,直径为2a的圆中有一个正方形,那么阴影部分的面积为( )
如图,直径为2a的圆中有一个正方形,那么阴影部分的面积为( )
 如图,直径为2a的圆中有一个正方形,那么阴影部分的面积为( )
如图,直径为2a的圆中有一个正方形,那么阴影部分的面积为( )| A. | (4-π)a2 | B. | (π-3)a2 | C. | (π-2.5)a2 | D. | (π-2)a2 |
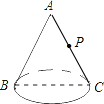 如图,有一个圆锥,它的底面半径是2cm,母线长是8cm,在点B处有一只蚂蚁,它想吃到与B点相对且离圆锥顶点3$\sqrt{2}$cm 的点P处的食物,蚂蚁爬行的最短路程是2$\sqrt{5}$cm.
如图,有一个圆锥,它的底面半径是2cm,母线长是8cm,在点B处有一只蚂蚁,它想吃到与B点相对且离圆锥顶点3$\sqrt{2}$cm 的点P处的食物,蚂蚁爬行的最短路程是2$\sqrt{5}$cm. 如图所示,在△ABC中,AB=AC,AD⊥BC于点D,AE∥BC,F是AD的中点,若AD=12,BC=16,求BE的长.
如图所示,在△ABC中,AB=AC,AD⊥BC于点D,AE∥BC,F是AD的中点,若AD=12,BC=16,求BE的长. 如图,AD∥BF,BE∥CG,∠DAB=45°,∠BCG=110°,求∠EBF的度数.
如图,AD∥BF,BE∥CG,∠DAB=45°,∠BCG=110°,求∠EBF的度数.