题目内容
9.已知关于x的一元二次方程x2-3x+k-1=0有实数根,k为正整数.(1)求正整数k的值;
(2)若此方程有两个不为0的整数根,请求出此时k的值及这两个整数根;
(3)在(2)的条件下,将关于x的二次函数y=x2-3x+k-1的图象向下平移2个单位,求平移后的函数图象的解析式.
分析 (1)根据一元二次方程x2-3x+k-1=0有实数根,可推△≥0,根据k为正整数,可确定k的数值;
(2)分别把k的正整数值代入方程x2-3x+k-1=0,解得结果进行分析解答;
(3)求出符合要求的k值,结合抛物线平移的规律写出其平移后的解析式.
解答 解:(1)∵方程x2-3x+k-1=0有实数根,
∴△=9-4(k-1)≥0,
∴k≤$\frac{13}{4}$.
又∵k为正整数,
∴k=1或2或3.
(2)当此方程有两个非零的整数根时,
当k=1时,方程为x2-3x=0,解得x1=0,x2=3;不合题意,舍去.
当k=2时,方程为x2-3x+1=0,解得x1=$\frac{3+\sqrt{5}}{2}$,x2=$\frac{3-\sqrt{5}}{2}$;不合题意,舍去.
当k=3时,方程为x2-3x+2=0,解得x1=1,x2=-2;符合题意.
(3)二次函数y=x2-3x+2的图象向下平移2个单位得到y=x2-3x.
点评 此题考查了一元二次方程根的判别式,解一元二次方程,二次函数平移的性质,求得方程的整数根是解决问题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
18.在Rt△ABC中,∠BAC=90°,AB=3,BC=5,若将Rt△ABC绕直线BC旋转一周,则所得立体图形的侧面积为 ( )
| A. | 6π | B. | 9π | C. | 15π | D. | $\frac{84}{5}$π |
19.下列说法不正确的是( )
| A. | 增加几次实验,事件发生的频率与这一事件发生的概率的差距可能扩大 | |
| B. | 增加几次实验,事件发生的频率越来越接近这一事件发生的概率的差距可能缩小 | |
| C. | 实验次数很大时,事件发生的频率稳定在这一事件发生的概率附近 | |
| D. | 实验次数增大时,事件发生的频率越来越接近这一事件发生的概率 |
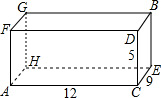 有一长方体纸盒,如图所示,小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长为12,宽为9,高为5,请你帮助该小组计算出由A到B的最短路线.(21.592≈466,18.442≈340,结果保留两位小数)
有一长方体纸盒,如图所示,小明所在的数学兴趣小组研究由长方体的底面A点到长方体中与A点相对的B点最短距离.若长方体的底面边长为12,宽为9,高为5,请你帮助该小组计算出由A到B的最短路线.(21.592≈466,18.442≈340,结果保留两位小数)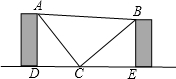 一个等腰直角三角板如图搁置在两柜之间,且点D,C,E在同一直线上,已知稍高的柜高AD为80cm,两柜距离DE为140cm.求稍矮的柜高BE.
一个等腰直角三角板如图搁置在两柜之间,且点D,C,E在同一直线上,已知稍高的柜高AD为80cm,两柜距离DE为140cm.求稍矮的柜高BE.