题目内容
如图，四边形ABCD是平行四边形，∠ABC=65°，BE平分∠ABC且交AD于E，DF∥BE，交BC于F．求∠CDF的大小．考点：平行四边形的性质
专题：
分析：根据已知条件和平行四边形的判定方法可证明四边形EBFD是平行四边形，进而得到∠CDF=∠ABE的度数．
解答：解：∵四边形ABCD是平行四边形，
∴DE∥BF，
∵DF∥BE，
∴四边形EBFD是平行四边形，
∴∠EBF=∠EDF，
∴∠CDF=∠ABR，
∵∠ABC=65°，BE平分∠ABC且交AD于E，
∴∠ABE=32.5°，
∴∠CDF=32.5°．
∴DE∥BF，
∵DF∥BE，
∴四边形EBFD是平行四边形，
∴∠EBF=∠EDF，
∴∠CDF=∠ABR，
∵∠ABC=65°，BE平分∠ABC且交AD于E，
∴∠ABE=32.5°，
∴∠CDF=32.5°．
点评：本题主要考查平行四边形的性质及角平分线的性质问题，要熟练掌握，并能够求解一些简单的计算、证明问题．
练习册系列答案
相关题目
如图，△ABC和△CDE均为等腰直角三角形，点B，C，D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=
完成下面推理过程：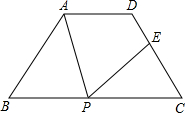
如图，等腰梯形ABCD中，AD∥BC，AD=3cm，BC=7cm，∠B=60°，P为下底上一点（不与B、C重合），连结AP，过P点作PE交DC于E，使得∠APE=B．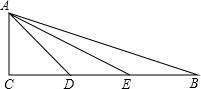
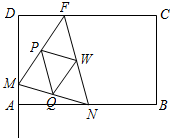如图，矩形ABCD的边AB=6cm，BC=4cm，点F在DC上，DF=2cm．动点M、N分别从点D、B同时出发，沿射线DA、线段BA向点A的方向运动（点M可运动到DA的延长线上），当动点N运动到点A时，M、N两点同时停止运动．连接FM、FN，当F、N、M不在同一直线时，可得△FMN，再连接△FMN三边的中点得
如图，已知菱形AOBD的A、B、D三点在⊙O上，延长BO至点P，交⊙O于点C，且BP=3OB．