题目内容
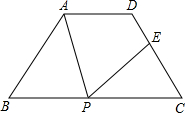 如图,等腰梯形ABCD中,AD∥BC,AD=3cm,BC=7cm,∠B=60°,P为下底上一点(不与B、C重合),连结AP,过P点作PE交DC于E,使得∠APE=B.
如图,等腰梯形ABCD中,AD∥BC,AD=3cm,BC=7cm,∠B=60°,P为下底上一点(不与B、C重合),连结AP,过P点作PE交DC于E,使得∠APE=B.(1)求证:△ABP∽△PCE;
(2)若BP=1cm,求点E分DC所成的比?
考点:相似三角形的判定与性质,等腰梯形的性质
专题:
分析:(1)由等腰梯形ABCD中,AD∥BC,AB=CD,可得∠B=∠C=60°,又由∠APE+∠EPC=∠B+∠BAP,∠APE=∠B,可证得∠BAP=∠EPC,根据有两角对应相等的三角形相似,即可证得:△APB∽△PEC;
(2)首先过点D作DF⊥BC交BC于点F,得出CF=2cm,又由△APB∽△PEC,根据相似三角形的对应边成比例,即可求得答案.
(2)首先过点D作DF⊥BC交BC于点F,得出CF=2cm,又由△APB∽△PEC,根据相似三角形的对应边成比例,即可求得答案.
解答:(1)证明:∵等腰梯形ABCD中,AD∥BC,AB=CD,
∴∠B=∠C=60°,
∵∠APC=∠B+∠BAP,
即∠APE+∠EPC=∠B+∠BAP,
∵∠APE=∠B,
∴∠BAP=∠EPC,
∴△APB∽△PEC;
(2)解:如图,

过点D作DF⊥BC交BC于点F,
则CF=2cm,
在Rt△DCF中,∠C=60°,CF=2cm,
∴DC=4cm,
∵△APB∽△PEC,
∴
=
,
即
=
,
∴EC=
cm,DE=
cm.
∴∠B=∠C=60°,
∵∠APC=∠B+∠BAP,
即∠APE+∠EPC=∠B+∠BAP,
∵∠APE=∠B,
∴∠BAP=∠EPC,
∴△APB∽△PEC;
(2)解:如图,

过点D作DF⊥BC交BC于点F,
则CF=2cm,
在Rt△DCF中,∠C=60°,CF=2cm,
∴DC=4cm,
∵△APB∽△PEC,
∴
| AB |
| PC |
| BP |
| EC |
即
| 4 |
| 6 |
| 1 |
| EC |
∴EC=
| 3 |
| 2 |
| 5 |
| 2 |
点评:此题考查了等腰梯形的性质、相似三角形的判定与性质.注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
下列调查方式中,最适合的是( )
| A、环保部门调查新安江屯溪段的水质情况,采用抽样调查方式 |
| B、调查你所在班级同学的视力情况,采用抽样调查方式 |
| C、调查黄山市中学生每天的就寝时间,采用全面调查方式 |
| D、调查黄山电视台的收视率,采用全面调查方式 |
下列说法正确的是( )
A、在一次抽奖活动中,“中奖的概率是
| ||
| B、随机抛一枚硬币,落地后正面朝上是一个必然事件 | ||
| C、从1,2,3,4,5中随机抽取一个数,抽到偶数的概率较大 | ||
D、在一副没有大小王的扑克牌中任意抽一张,抽到的牌是6的概率是
|
 如图,四边形ABCD是平行四边形,∠ABC=65°,BE平分∠ABC且交AD于E,DF∥BE,交BC于F.求∠CDF的大小.
如图,四边形ABCD是平行四边形,∠ABC=65°,BE平分∠ABC且交AD于E,DF∥BE,交BC于F.求∠CDF的大小. 如图,在矩形ABCD中,AB=6m,BC=8m,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点O以1米/秒的速度从点C出发,沿CB向点B移动,设PO两点移动t秒后(0<t<5)后,△POC的面积为S米2.
如图,在矩形ABCD中,AB=6m,BC=8m,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点O以1米/秒的速度从点C出发,沿CB向点B移动,设PO两点移动t秒后(0<t<5)后,△POC的面积为S米2.