题目内容
如图,在Rt△ABC中,∠C=90°,且AC=CD=
,又E,D为CB的三等分点.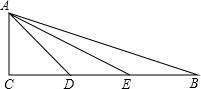
(1)证明:△ADE∽△BDA;
(2)证明:∠ADC=∠AEC+∠B;
(3)若点P为线段AB上一动点,连接PE,则使得线段PE的长度为整数的点P的个数有几个?请说明理由.
| 2 |

(1)证明:△ADE∽△BDA;
(2)证明:∠ADC=∠AEC+∠B;
(3)若点P为线段AB上一动点,连接PE,则使得线段PE的长度为整数的点P的个数有几个?请说明理由.
考点:相似三角形的判定与性质
专题:
分析:(1)由AC=CD=DE=EB=
,∠C=90°,利用勾股定理易求AD=2,从而可求
=
=
,又∠ADE=∠BDA,那么可证△ADE∽△BDA;
(2)由于△ADE∽△BDA,利用形似三角形的性质可知∠DAE=∠B,再由三角形外角定义可知∠ADC=∠AEC+∠DAE,等量代换即可证明;
(3)在直角三角形ACD中,由AC与CE,利用勾股定理求出AE的长,根据AE与△ABE中AB边高的长,确定出PE的范围,即可得出PE为整数的点P的个数.
| 2 |
| DE |
| AD |
| DA |
| BD |
| ||
| 2 |
(2)由于△ADE∽△BDA,利用形似三角形的性质可知∠DAE=∠B,再由三角形外角定义可知∠ADC=∠AEC+∠DAE,等量代换即可证明;
(3)在直角三角形ACD中,由AC与CE,利用勾股定理求出AE的长,根据AE与△ABE中AB边高的长,确定出PE的范围,即可得出PE为整数的点P的个数.
解答: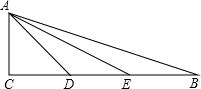 (1)证明:∵AC=CD=DE=EB=
(1)证明:∵AC=CD=DE=EB=
,
又∠C=90°,
∴AD=2,
∴
=
,
=
=
,
∴
=
,
又∵∠ADE=∠BDA,
∴△ADE∽△BDA;
(2)证明:∵△ADE∽△BDA,
∴∠DAE=∠B,
又∵∠ADC=∠AEC+∠DAE,
∴∠ADC=∠AEC+∠B;
(3)解:∵点P为线段AB上一动点,
根据勾股定理得:AE=
=
,BE=
,
∴PE的最大值为
.
作EF⊥AB,则EF=
,则PE的最小值为
∴
≤EP≤
,
∵EP为整数,即EP=1,2,3,
结合图形可知PE=1时有两个点,
所以PE长为整数的点P个数为4个.
 (1)证明:∵AC=CD=DE=EB=
(1)证明:∵AC=CD=DE=EB=| 2 |
又∠C=90°,
∴AD=2,
∴
| DE |
| AD |
| ||
| 2 |
| DA |
| BD |
| 2 | ||
2
|
| ||
| 2 |
∴
| DE |
| AD |
| DA |
| BD |
又∵∠ADE=∠BDA,
∴△ADE∽△BDA;
(2)证明:∵△ADE∽△BDA,
∴∠DAE=∠B,
又∵∠ADC=∠AEC+∠DAE,
∴∠ADC=∠AEC+∠B;
(3)解:∵点P为线段AB上一动点,
根据勾股定理得:AE=
| AC2+CE2 |
| 10 |
| 2 |
∴PE的最大值为
| 10 |
作EF⊥AB,则EF=
| ||
| 5 |
| ||
| 5 |
∴
| ||
| 5 |
| 10 |
∵EP为整数,即EP=1,2,3,
结合图形可知PE=1时有两个点,
所以PE长为整数的点P个数为4个.
点评:本题考查了勾股定理、相似三角形的判定和性质、三角形外角定义,如果两个三角形两组对应边成比例,且夹角相等则两三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若m、n是方程ax2+bx+c=0(a≠0)的两个实数根,设M=2am+b、N=2an+b,则M、N的关系是( )
| A、M>N | B、M<N |
| C、M+N=0 | D、M=N |
a2b-4ab+4b因式分解为( )
| A、(a-2)2b |
| B、(2a-2)2b |
| C、(2a-1)2b |
| D、(a+2)2b |
 如图,在△ABC中,DE∥BC,AD=3DB,△ABC的面积为72.求:△ADE的面积、四边形DEBC的面积.
如图,在△ABC中,DE∥BC,AD=3DB,△ABC的面积为72.求:△ADE的面积、四边形DEBC的面积. 如图,四边形ABCD是平行四边形,∠ABC=65°,BE平分∠ABC且交AD于E,DF∥BE,交BC于F.求∠CDF的大小.
如图,四边形ABCD是平行四边形,∠ABC=65°,BE平分∠ABC且交AD于E,DF∥BE,交BC于F.求∠CDF的大小.