题目内容
3.在二次函数y=ax2+bx+c(a≠0)中,函数y与自变量x的部分对应值如下表:| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
分析 观察表格发现函数的图象经过点(0,-6)和(1,-6),根据两点的纵坐标相同,说明两点关于对称轴对称,从而求解.
解答 解:观察表格发现函数的图象经过点(0,-6)和(1,-6),
∵两点的纵坐标相同,
∴两点关于对称轴对称,
∴对称轴为:x=$\frac{0+1}{2}$=$\frac{1}{2}$,
∴满足x<$\frac{1}{2}$时,y随x的增大而增大
∴故答案为:x<$\frac{1}{2}$.
点评 本题考查了二次函数的性质,了解(0,-6)和(1,-6),两点关于对称轴对称是解决本题的关键.

练习册系列答案
相关题目
16.一辆出租车从某地出发,在一条东西走向的接到上往返行驶,每次行驶的路程(记向东为正),记录如下(8<x<24,单位:km);
(1)说出这辆出租车每次行驶的方向;
(2)这辆出租车一共行驶了多少路程(用含x的式子表示)?
| 第一次 | 第二次 | 第三次 | 第四次 |
| x | 3(8-x) | x-6 | -$\frac{2}{3}$x |
(2)这辆出租车一共行驶了多少路程(用含x的式子表示)?
15.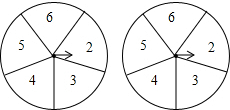 如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
 如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )
如图的两个圆盘中均有5个数字,同时旋转两个圆盘,指针落在某一个数上的机会均等,那么两个指针同时落在奇数上的概率是( )| A. | $\frac{4}{25}$ | B. | $\frac{6}{25}$ | C. | $\frac{10}{25}$ | D. | $\frac{19}{25}$ |
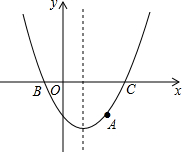 已知:二次函数的图象经过A(2,-3),对称轴x=1,抛物线与x轴两交点B、C的距离为4.
已知:二次函数的图象经过A(2,-3),对称轴x=1,抛物线与x轴两交点B、C的距离为4.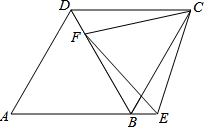 如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:
如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证: