题目内容
18.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c三边,则下列式子一定成立的是( )| A. | a=c•sinB | B. | a=c•cosB | C. | $c=\frac{a}{tanB}$ | D. | c=a•sinA |
分析 本题可以利用锐角三角函数的定义代入求解即可.
解答 解:在RT△ABC中,∠C=90°,
则cosA=$\frac{b}{c}$,sinA=$\frac{a}{c}$,tanB=$\frac{b}{a}$,cosB=$\frac{a}{c}$,tanA=$\frac{a}{b}$,cotA=$\frac{b}{a}$.
因而b=c•cosA=a•tanB,a=c•sinA=c•cosB=b•tanA,
所以,一定成立的是a=c•cosB.
故选B
点评 此题考查锐角三角函数,关键是利用锐角三角函数的定义,正确理解直角三角形边角之间的关系.在直角三角形中,如果已知一边及其中的一个锐角,就可以表示出另外的边.

练习册系列答案
相关题目
8.为了解某市数学中考成绩,从中随机抽取了3000名考生进行调查,这项调查中的样本是( )
| A. | 某市数学中考成绩 | |
| B. | 从中抽取的3000名考生 | |
| C. | 从中抽取的3000名考生的数学中考成绩 | |
| D. | 3000 |
6.方程-4x=1的解是( )
| A. | $x=-\frac{1}{4}$ | B. | x=-4 | C. | $x=\frac{1}{4}$ | D. | x=-4. |
13.对于四边形的以下说法:其中正确的个数有( )
①对角线互相平分的四边形是平行四边形;
②对角线相等且互相平分的四边形是矩形;
③对角线垂直且互相平分的四边形是菱形;
④顺次连结对角线相等的四边形各边的中点所得到的四边形是矩形.
①对角线互相平分的四边形是平行四边形;
②对角线相等且互相平分的四边形是矩形;
③对角线垂直且互相平分的四边形是菱形;
④顺次连结对角线相等的四边形各边的中点所得到的四边形是矩形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.如果关于x的不等式(m+1)x>m+1的解集为x<1,则m的取值范围是( )
| A. | m<0 | B. | m<-1 | C. | m>1 | D. | m>-1 |
7.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}3x+2y=6\\ \frac{6}{x}-2y=5\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+3y=6\\ y-z=5\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}2x+5y=7\\ xy=5\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+2y=5\\ 3x-2y-5=0\end{array}\right.$ |
8.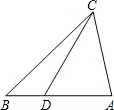 如图,要使△ACD∽△ABC,需要补充的一个条件是( )
如图,要使△ACD∽△ABC,需要补充的一个条件是( )
 如图,要使△ACD∽△ABC,需要补充的一个条件是( )
如图,要使△ACD∽△ABC,需要补充的一个条件是( )| A. | $\frac{AC}{CD}$=$\frac{BA}{BC}$ | B. | $\frac{CD}{AD}$=$\frac{BC}{AC}$ | C. | CD2=AD•DB | D. | AC2=AD•AB |
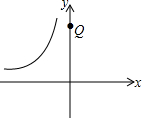 对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+$\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+$\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.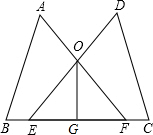 如图,点E、F在BC上,BE=CF,AB=CD,∠B=∠C,AF与DE交于点O,G为EF中点.求证:OG⊥EF.
如图,点E、F在BC上,BE=CF,AB=CD,∠B=∠C,AF与DE交于点O,G为EF中点.求证:OG⊥EF.