题目内容
17．
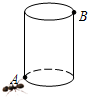如图，有一个底边半径为6cm，高为24cm的圆柱，在圆柱下底面的点A处有一只蚂蚁，它想吃到上底面上与A点相对的B处的食物，试问：它需要爬行的最短路程越是多少？
分析 要想求得最短路程，首先要把A和B展开到一个平面内．根据两点之间，线段最短求出蚂蚁爬行的最短路程．
解答 解：如图，将圆柱体展开，连接A、B，根据两点之间线段最短，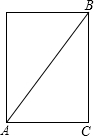
根据题意可得：BC=24cm，AC是圆周的一半，
∴AC=$\frac{1}{2}$×2×π×6=18cm，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=30cm，
∴它需爬行的最短路程约是30cm．
点评 此题主要考查了最短路径问题，求两个不在同一平面内的两个点之间的最短距离时，一定要展开到一个平面内是解题关键．
练习册系列答案
高中必刷题系列答案
相关题目
7．下列方程组中，是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}3x+2y=6\\ \frac{6}{x}-2y=5\end{array}\right.$ | B． | $\left\{\begin{array}{l}x+3y=6\\ y-z=5\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}2x+5y=7\\ xy=5\end{array}\right.$ | D． | $\left\{\begin{array}{l}x+2y=5\\ 3x-2y-5=0\end{array}\right.$ |
8．
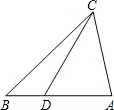如图，要使△ACD∽△ABC，需要补充的一个条件是（ ）
如图，要使△ACD∽△ABC，需要补充的一个条件是（ ）| A． | $\frac{AC}{CD}$=$\frac{BA}{BC}$ | B． | $\frac{CD}{AD}$=$\frac{BC}{AC}$ | C． | CD2=AD•DB | D． | AC2=AD•AB |
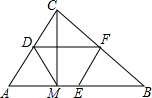如图，已知D、E、F为△ABC的三边的中点，CM⊥AB．
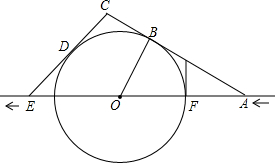如图，某船在大海中沿航线由东向西行驶，行驶到A时，发现前方20海里的F处出现暗礁，经进一步观察发现前方以点O为圆心（点O在航线上），OF长为半径的区域内充满暗礁，该船马上改变航向，从点A沿北偏西60°方向前进，与⊙O切于点B后到达点C，接着，该船从点C沿南偏西45°方向前进，与⊙O切于点D后回到航线上点E，然后继续沿原航线行驶，请解决下列问题：暗礁区域的半径为多少海里？
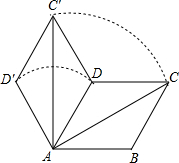如图，菱形ABCD的边长为4，∠BAD=60°，AC为对角线．将△ACD绕点A逆时针旋转60°得到△AC′D′，连结DC′．
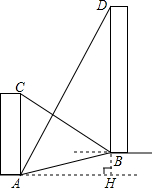如图，AC、BD是一斜坡AB上的两幢楼房，斜坡AB的坡度是1：2$\sqrt{3}$，从点A测得楼BD顶部D处的仰角60°，从点B测得楼AC顶部C处的仰角30°，楼BD自身高度BD比楼AC高12米，求楼AC和楼BD之间的水平距离？（结果保留根号）
7．一元二次方程x2+2=0的根的情况为（ ）
| A． | 没有实根 | B． | 有两个相等的实根 | ||
| C． | 有两个不等的实根 | D． | 有两个实根 |