题目内容
16.已知函数y1=2x-3,y2=-x+3.(1)在同一坐标系中画出这两个函数的图象.
(2)求出函数图象与x轴围成三角形的面积.
分析 (1)先求出直线y1=2x-3,y2=-x+3与x轴和y轴的交点,再画出两函数图象即可;
(2)根据三角形的面积公式求解即可.
解答 解:(1)函数y1=2x-3与x轴和y轴的交点是(1.5,0)和(0,-3),y2=-x+3与x轴和y轴的交点是(3,0)和(0,3),其图象如图: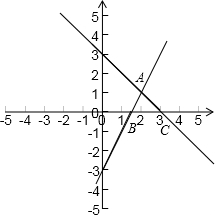
(2)设y1=2x-3,y2=-x+3的交点为点A,可得:$\left\{\begin{array}{l}{y=2x-3}\\{y=-x+3}\end{array}\right.$,
可得:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
S△ABC=$\frac{1}{2}$BC•1=$\frac{1}{2}$×(3-1.5)×1=$\frac{3}{4}$.
点评 本题考查的是一次函数的图象,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
6.方程-4x=1的解是( )
| A. | $x=-\frac{1}{4}$ | B. | x=-4 | C. | $x=\frac{1}{4}$ | D. | x=-4. |
7.下列方程组中,是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}3x+2y=6\\ \frac{6}{x}-2y=5\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+3y=6\\ y-z=5\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}2x+5y=7\\ xy=5\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+2y=5\\ 3x-2y-5=0\end{array}\right.$ |
8.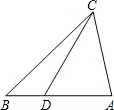 如图,要使△ACD∽△ABC,需要补充的一个条件是( )
如图,要使△ACD∽△ABC,需要补充的一个条件是( )
 如图,要使△ACD∽△ABC,需要补充的一个条件是( )
如图,要使△ACD∽△ABC,需要补充的一个条件是( )| A. | $\frac{AC}{CD}$=$\frac{BA}{BC}$ | B. | $\frac{CD}{AD}$=$\frac{BC}{AC}$ | C. | CD2=AD•DB | D. | AC2=AD•AB |
 如图,一个长方形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE的度数是125°,则∠DBC=55°.
如图,一个长方形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE的度数是125°,则∠DBC=55°.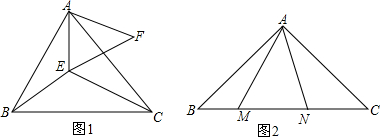
 如图是用吸管吸易拉罐内的饮料时的横截面,若∠1=110°,则∠2=70°.(易拉罐的上下底面互相平行)
如图是用吸管吸易拉罐内的饮料时的横截面,若∠1=110°,则∠2=70°.(易拉罐的上下底面互相平行)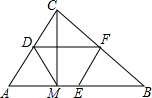 如图,已知D、E、F为△ABC的三边的中点,CM⊥AB.
如图,已知D、E、F为△ABC的三边的中点,CM⊥AB.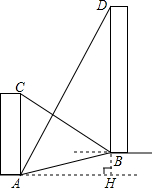 如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2$\sqrt{3}$,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)
如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2$\sqrt{3}$,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)