题目内容
3.(1)(-a3)2•(-a2)3(2)-t3•(-t)4•(-t)5
(3)(p-q)4÷(q-p)3•(p-q)2
(4)30-2-3+(-3)2-($\frac{1}{4}$)-1
(5)(-9)3×(-$\frac{2}{3}$)3×($\frac{1}{3}$)3
(6)-0.2514×230.
分析 (1)根据同底数幂的乘法的性质,幂的乘方的性质,即可解答.
(2)根据同底数幂的乘法的性质,即可解答.
(3)根据同底数幂的乘法、除法的性质,即可解答.
(4)根据0次幂,负整数指数幂,即可解答.
(5)先算乘方,再进行乘法计算,即可解答.
(6)根据同底数幂的乘法的性质,幂的乘方的性质,积的乘方的性质,即可解答.
解答 解:(1)(-a3)2•(-a2)3
=a6•(-a6)
=-a12.
(2)-t3•(-t)4•(-t)5
=-t3•t4•(-t5)
=t12.
(3)(p-q)4÷(q-p)3•(p-q)2
=(p-q)4-3+2
=(p-q)3.
(4)30-2-3+(-3)2-($\frac{1}{4}$)-1
=1$-\frac{1}{8}+9-4$
=5$\frac{7}{8}$.
(5)(-9)3×(-$\frac{2}{3}$)3×($\frac{1}{3}$)3
=${9}^{3}×\frac{8}{27}×\frac{1}{27}$
=8.
(6)-0.2514×230
=-(0.25×2)14×216
=-$\frac{1}{{2}^{14}}×{2}^{16}$
=-4.
点评 本题考查了同底数幂的乘法,幂的乘方,积的乘方,理清指数的变化是解题的关键.

练习册系列答案
相关题目
13.对于四边形的以下说法:其中正确的个数有( )
①对角线互相平分的四边形是平行四边形;
②对角线相等且互相平分的四边形是矩形;
③对角线垂直且互相平分的四边形是菱形;
④顺次连结对角线相等的四边形各边的中点所得到的四边形是矩形.
①对角线互相平分的四边形是平行四边形;
②对角线相等且互相平分的四边形是矩形;
③对角线垂直且互相平分的四边形是菱形;
④顺次连结对角线相等的四边形各边的中点所得到的四边形是矩形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.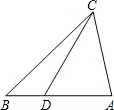 如图,要使△ACD∽△ABC,需要补充的一个条件是( )
如图,要使△ACD∽△ABC,需要补充的一个条件是( )
 如图,要使△ACD∽△ABC,需要补充的一个条件是( )
如图,要使△ACD∽△ABC,需要补充的一个条件是( )| A. | $\frac{AC}{CD}$=$\frac{BA}{BC}$ | B. | $\frac{CD}{AD}$=$\frac{BC}{AC}$ | C. | CD2=AD•DB | D. | AC2=AD•AB |
15.在△ABC中,AB2=2BC2,AC=BC,那么∠A:∠B:∠C为( )
| A. | 1:2:3 | B. | 2:1:3 | C. | 1:1:2 | D. | 1:2:1 |