题目内容
20.【试题再现】如图1,Rt△ABC中,∠ACB=90°,AC=BC,直线l过点C,过点A、B分别作AD⊥l于点D,BE⊥l于点E,则DE=AD+BE(不用证明).(1)【类比探究】如图2,在△ABC中,AC=BC,且∠ACB=∠ADC=∠BEC=100°,上述结论是否成立?若成立,请说明理由:若不成立,请写出一个你认为正确的结论.
(2)【拓展延伸】①如图3,在△ABC中,AC=nBC,且∠ACB=∠ADC=∠BEC=100°,猜想线段DE、AD、BE之间有什么数量关系?并证明你的猜想.
②若图1的Rt△ABC中,∠ACB=90°,AC=nBC,并将直线l绕点C旋转一定角度后与斜边AB相交,分别过点A、B作直线l的垂线,垂足分别为点D和点E,请在备用图上画出图形,并直接写出线段DE、AD、BE之间满足的一种数量关系(不要求写出证明过程).
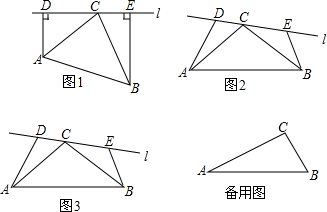
分析 (1)易证△ACD≌△CBE,则有AD=CE,CD=BE,从而可得DE=AD+BE;
(2)①易证△ADC∽△CEB,则有$\frac{AD}{CE}$=$\frac{CD}{BE}$=$\frac{AC}{BC}$=n,从而可得CE=$\frac{1}{n}$AD,CD=nBE,即可得到DE=DC+CE=$\frac{1}{n}$AD+nBE;
②同①可得CE=$\frac{1}{n}$AD,CD=nBE.由于直线l在绕着点C旋转过程中,点A到直线l的距离AD与点B到直线l的距离BE大小关系会发生变化,因此需分情况讨论(如图4、图5),然后只需结合图形就可解决问题.
解答 解:(1)【类比探究】猜想DE=AD+BE.
理由:如图2,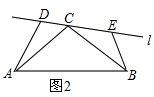
∵∠ADC=100°,
∴∠DAC+∠DCA=80°.
∵∠ACB=100°,
∴∠DCA+∠ECB=80°,
∴∠DAC=∠ECB.
在△ACD和△CBE中,
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠DAC=∠ECB}\\{AC=CB}\end{array}\right.$,
∴△ACD≌△CBE,
∴AD=CE,CD=BE,
∴DE=AD+BE;
(2)【拓展延伸】①猜想:DE=$\frac{1}{n}$AD+nBE.
理由:如图3,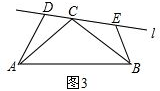
∵∠ADC=100°,
∴∠DAC+∠DCA=80°.
∵∠ACB=100°,
∴∠DCA+∠ECB=80°,
∴∠DAC=∠ECB.
∵∠ADC=∠CEB,
∴△ADC∽△CEB,
∴$\frac{AD}{CE}$=$\frac{CD}{BE}$=$\frac{AC}{BC}$=n,
∴CE=$\frac{1}{n}$AD,CD=nBE,
∴DE=DC+CE=$\frac{1}{n}$AD+nBE;
②DE=$\frac{1}{n}$AD-nBE或DE=nBE-$\frac{1}{n}$AD.
提示:同①可得:CE=$\frac{1}{n}$AD,CD=nBE.
如图4,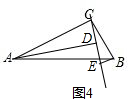
DE=CE-CD=$\frac{1}{n}$AD-nBE;
如图5,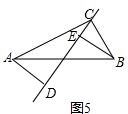
DE=CD-DE=nBE-$\frac{1}{n}$AD.
点评 本题是一道探究题,用到了全等三角形的判定与性质、相似三角形的判定与性质、三角形的内角和定理、平角的定义等知识,考查了探究能力,渗透了分类讨论的思想以及特殊到一般的思想,是一道好题.

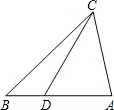 如图,要使△ACD∽△ABC,需要补充的一个条件是( )
如图,要使△ACD∽△ABC,需要补充的一个条件是( )| A. | $\frac{AC}{CD}$=$\frac{BA}{BC}$ | B. | $\frac{CD}{AD}$=$\frac{BC}{AC}$ | C. | CD2=AD•DB | D. | AC2=AD•AB |
| A. | 1:2:3 | B. | 2:1:3 | C. | 1:1:2 | D. | 1:2:1 |
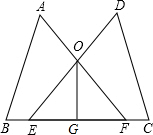 如图,点E、F在BC上,BE=CF,AB=CD,∠B=∠C,AF与DE交于点O,G为EF中点.求证:OG⊥EF.
如图,点E、F在BC上,BE=CF,AB=CD,∠B=∠C,AF与DE交于点O,G为EF中点.求证:OG⊥EF.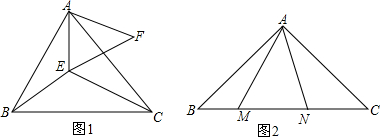
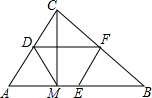 如图,已知D、E、F为△ABC的三边的中点,CM⊥AB.
如图,已知D、E、F为△ABC的三边的中点,CM⊥AB.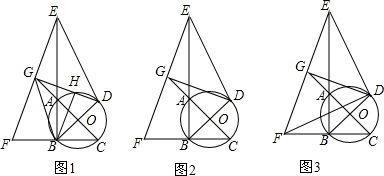
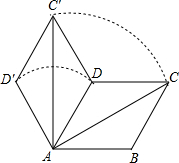 如图,菱形ABCD的边长为4,∠BAD=60°,AC为对角线.将△ACD绕点A逆时针旋转60°得到△AC′D′,连结DC′.
如图,菱形ABCD的边长为4,∠BAD=60°,AC为对角线.将△ACD绕点A逆时针旋转60°得到△AC′D′,连结DC′.