题目内容
3.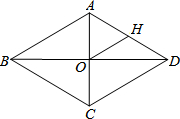 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,OH=8,则菱形ABCD的周长等于64.
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,OH=8,则菱形ABCD的周长等于64.
分析 先根据菱形的性质得出AC⊥BD,AB=AD=CD=BC,再由直角三角形的性质求出AD的长,进而可得出结论.
解答 解:∵四边形ABCD是菱形,对角线AC、BD相交于点O,
∴AC⊥BD,AB=AD=CD=BC.
∵H为AD边中点,OH=8,
∴AD=16,
∴菱形ABCD的周长=4AD=64.
故答案为:64.
点评 本题考查的是菱形的性质,熟知菱形的对角线互相垂直是解答此题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
11.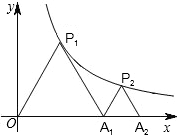 如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
 如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )
如图,点P1,P2在反比例函数y=$\frac{1}{x}$(x>0)的图象上,△P1OA1,△P2A1A2,都是等腰直角三角形,斜边OA1,A1A2在x轴上,则A1A2的长为( )| A. | -1+$\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | -2+2$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
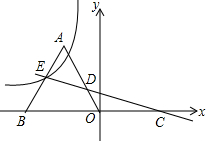 如图,△ABO为等边三角形,点B的坐标为(-4,0),过点C(4,0)作直线l交AO于点D,交AB于点E,点E在反比例函数y=$\frac{k}{x}$ (x<0)的图象上,且△ADE的面积和△DOC的面积相等,则k的值是-3$\sqrt{3}$.
如图,△ABO为等边三角形,点B的坐标为(-4,0),过点C(4,0)作直线l交AO于点D,交AB于点E,点E在反比例函数y=$\frac{k}{x}$ (x<0)的图象上,且△ADE的面积和△DOC的面积相等,则k的值是-3$\sqrt{3}$. 如图,已知?ABCD,AB=$\frac{1}{2}$BC,延长AB至F,使BF=AB,再延长BA至E,使AE=AB,试判断EC与FD的位置关系,并说明其结论正确的理由.
如图,已知?ABCD,AB=$\frac{1}{2}$BC,延长AB至F,使BF=AB,再延长BA至E,使AE=AB,试判断EC与FD的位置关系,并说明其结论正确的理由.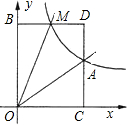 如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D. 在?ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm.
在?ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm.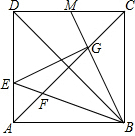 如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.
如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.