题目内容
12.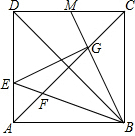 如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.
如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.(1)求DE:CG的值;
(2)设AE=x,S△BEG=y.
①求y关于x的函数表达式及x的取值范围.
②当图中点E、M关于对角线BD成轴对称时,求y的值.
分析 (1)由四边形ABCD为正方形,得到∠BDE=∠BCG=∠CBD=45°,BD=$\sqrt{2}$BC,再由∠EBM=45°,利用等式的性质得到一对角相等,利用两对角相等的三角形相似得到三角形BDE与三角形BCG相似,利用相似三角形对应边成比例即可求出所求;
(2)①由四边形ABCD为正方形,且三角形BDE与三角形BCG相似,得到对应边成比例,进而确定出三角形BEG与三角形BAD相似,得到三角形BEG为等腰直角三角形,表示出y与x的函数解析式即可;
②若E、M关于对角线BD成轴对称,连接EM,交AC于点H,可得BD垂直平分EM,BE为角平分线,进而得到AE=HE=DH,求出x的值,代入计算即可求出y的值.
解答 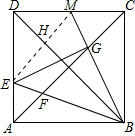 解:(1)∵四边形ABCD是正方形,
解:(1)∵四边形ABCD是正方形,
∴∠BDE=∠BCG=∠CBD=45°,BD=$\sqrt{2}$BC,
∵∠EBM=45°,
∴∠DBE=∠CBG,
∴△BDE∽△BCG,
∴DE:CG=BD:BC=$\sqrt{2}$:1;
(2)①∵四边形ABCD是正方形,且△BDE∽△BCG,
∴BE:BG=BD:BC=BD:AB=$\sqrt{2}$:1,
∴△BEG∽△BAD,
∴△BEG为等腰直角三角形,
∴y=S△BEG=$\frac{1}{4}$x2+9(0<x<6);
②若E、M关于对角线BD成轴对称,连接EM,交BD于点H,
∴BD垂直平分EM,BE平分∠ABD,
∴AE=HE=DH,DE=$\sqrt{2}$HE,
∴6-x=$\sqrt{2}$x,即x=6$\sqrt{2}$-6,
则y=$\frac{1}{4}$×(6$\sqrt{2}$-6)2+9=36-18$\sqrt{2}$.
点评 此题属于四边形综合题,涉及的知识有:相似三角形的判定与性质,以及正方形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是下列选项中的( )
如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若点A,B,C中至少有一个点在圆内,且至少有一个点在圆外,则r的值可以是下列选项中的( )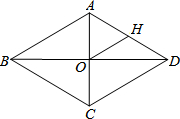 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,OH=8,则菱形ABCD的周长等于64.
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,OH=8,则菱形ABCD的周长等于64. 如图,E为?ABCD外的一点,AE=DE,BE=CE,AE⊥EC,BE⊥ED,四边形ABCD是矩形吗?请证明你的结论.
如图,E为?ABCD外的一点,AE=DE,BE=CE,AE⊥EC,BE⊥ED,四边形ABCD是矩形吗?请证明你的结论. 如图,平行四边形ABCD,AD=5,AB=6,点A的坐标为(-3,0),则点C的坐标为(6,4).
如图,平行四边形ABCD,AD=5,AB=6,点A的坐标为(-3,0),则点C的坐标为(6,4).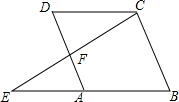 如图,?ABCD中,点E在BA的延长线上,CE交AD于F,求证:$\frac{DC}{BE}$=$\frac{DF}{BC}$.
如图,?ABCD中,点E在BA的延长线上,CE交AD于F,求证:$\frac{DC}{BE}$=$\frac{DF}{BC}$.