题目内容
8.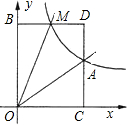 如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(2,1),点M(m,n)(0<m<2)是该函数图象上一动点,过点M作直线MB∥x轴,交y轴于点B,过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.(1)求反比例函数的解析式;
(2)当∠OAM=90°时,求点M的坐标.
分析 (1)把A点坐标代入y=$\frac{k}{x}$中求出k的值即可;
(2)先证明Rt△AMD∽Rt△OAC得到(n-1):2=(2-m):1,再利用点M(m,n)在y=$\frac{2}{x}$的图象上得到n=$\frac{2}{m}$,然后解关于m的方程求出m,从而可得到M点的坐标.
解答 解:(1)把A(2,1)代入y=$\frac{k}{x}$得k=2×1=2,
所以反比例函数解析式为y=$\frac{2}{x}$;
(2)∵∠OAM=90°,
∴∠MAD+∠CAO=90°,
而∠CAO+∠AOC=90°,
∴∠AOC=∠MAD,
∴Rt△AMD∽Rt△OAC,
∴AD:OC=MD:AC,即(n-1):2=(2-m):1,
∴n-1=4-2m,
∵点M(m,n)在y=$\frac{2}{x}$的图象上,
∴n=$\frac{2}{m}$,
∴$\frac{2}{m}$-1=4-2m,
整理得2m2-5m+2=0,解得m1=$\frac{1}{2}$,m2=2(舍去),
∴n=4,
∴点M的坐标为($\frac{1}{2}$,4).
点评 本题考查了用待定系数法求反比例函数的解析式:先设出含有待定系数的反比例函数解析式y=$\frac{k}{x}$(k为常数,k≠0);再把已知条件(自变量与函数的对应值)带入解析式,得到待定系数的方程;接着解方程,求出待定系数;然后写出解析式.解决(2)小题的关键是证明Rt△AMD∽Rt△OAC,利用相似比建立m与n的关系式.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
19.使不等式x-4>4x-1成立的值中最大的整数是( )
| A. | 0 | B. | -2 | C. | -1 | D. | 2 |
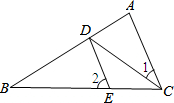 如图,已知CD平分∠ACB,DE∥AC,∠1=20°,则∠2=40°.
如图,已知CD平分∠ACB,DE∥AC,∠1=20°,则∠2=40°. 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数$y=\frac{k+1}{x}$的图象上.若点A的坐标为(-2,-2),则k的值为3.
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数$y=\frac{k+1}{x}$的图象上.若点A的坐标为(-2,-2),则k的值为3.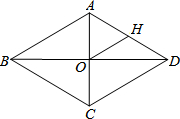 如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,OH=8,则菱形ABCD的周长等于64.
如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,OH=8,则菱形ABCD的周长等于64.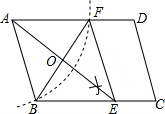 如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF. 如图,E为?ABCD外的一点,AE=DE,BE=CE,AE⊥EC,BE⊥ED,四边形ABCD是矩形吗?请证明你的结论.
如图,E为?ABCD外的一点,AE=DE,BE=CE,AE⊥EC,BE⊥ED,四边形ABCD是矩形吗?请证明你的结论.