题目内容
解方程组:
(1)
;
(2)2x-3y=4x+y=-6;
(3)
.
(1)
|
(2)2x-3y=4x+y=-6;
(3)
|
考点:解二元一次方程组,解三元一次方程组
专题:
分析:(1)把两个方程相加,消去y求出x的值,再代入第二个方程求出y即可;
(2)把式子化为
,再把第二个方程乘以3,与第一个相加消去y,求得x的值,再代入第二个方程即可得y的值;
(3)设
=
=
=k,于是得x=2k,y=3k,z=5k,代入第二个方程求得k的值,再求x、y、z即可.
(2)把式子化为
|
(3)设
| x |
| 2 |
| y |
| 3 |
| z |
| 5 |
解答:解:(1)
①+②,得3x=6
x=2,
把x=2代入②,得y=1,
所以原方程组的解为
;
(2)原方程化为
,
②×3,得12x+3y=-18③
①+③,得14x=-24
x=-
,
把x=-
代入②,得y=
,
所以原方程组的解为
;
(3)设
=
=
=k,
所以x=2k,y=3k,z=5k,
6k-3k+15k=-32
18k=-32
k=-
,
x=-
,y=
,z=-
,
所以原方程组的解为
.
|
①+②,得3x=6
x=2,
把x=2代入②,得y=1,
所以原方程组的解为
|
(2)原方程化为
|
②×3,得12x+3y=-18③
①+③,得14x=-24
x=-
| 12 |
| 7 |
把x=-
| 12 |
| 7 |
| 6 |
| 7 |
所以原方程组的解为
|
(3)设
| x |
| 2 |
| y |
| 3 |
| z |
| 5 |
所以x=2k,y=3k,z=5k,
6k-3k+15k=-32
18k=-32
k=-
| 16 |
| 9 |
x=-
| 32 |
| 9 |
| 16 |
| 3 |
| 80 |
| 9 |
所以原方程组的解为
|
点评:本题主要考查了解二元一次方程组、三元一次方程组.关键就是消元把三元一次方程组转化成二元一次方程组,把二元转化为一元.

练习册系列答案
相关题目
 如图,∠ACD=20°,DA=DB=DC,则∠ABC=( )
如图,∠ACD=20°,DA=DB=DC,则∠ABC=( )| A、50° | B、60° |
| C、70° | D、80° |
 如图,一枚棋子放在七边形A1A2A3A4A5A6A7的顶点A1处,现以逆时针方向沿着七边形的边移动这枚棋子,且规定:第一步从点A1处移动到A2处,第二步从点A2处移动到点A4处(在点A3处不停留),第三步从点A4处移动到AA7处(在点A5、A6处不停留),…,依此类推,若这枚棋子不停地这样一对下去,则这枚棋子永远不能停留的顶点有( )
如图,一枚棋子放在七边形A1A2A3A4A5A6A7的顶点A1处,现以逆时针方向沿着七边形的边移动这枚棋子,且规定:第一步从点A1处移动到A2处,第二步从点A2处移动到点A4处(在点A3处不停留),第三步从点A4处移动到AA7处(在点A5、A6处不停留),…,依此类推,若这枚棋子不停地这样一对下去,则这枚棋子永远不能停留的顶点有( )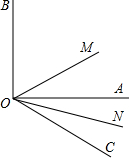 如图,∠AOB是直角,∠AOC=30°,ON是∠AOC的平分线,OM是∠BOC的平分线,求∠MON的度数.
如图,∠AOB是直角,∠AOC=30°,ON是∠AOC的平分线,OM是∠BOC的平分线,求∠MON的度数.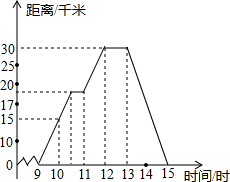 小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示).
小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示).